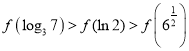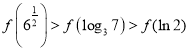题目内容
【题目】偶函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,不等式
,不等式![]() 在
在![]() 上有且只有200个整数解,则实数
上有且只有200个整数解,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据题意得到函数![]() 周期性,结合周期性将问题转化在一个周期
周期性,结合周期性将问题转化在一个周期![]() 内来研究,然后在结合函数图象的对称性将问题转化在
内来研究,然后在结合函数图象的对称性将问题转化在![]() 内研究,最后结合函数
内研究,最后结合函数![]() 在
在![]() 内整数解的个数及图象中的特殊点确定实数
内整数解的个数及图象中的特殊点确定实数![]() 的取值范围.
的取值范围.
详解:由![]() 得函数
得函数![]() 图象的对称轴为
图象的对称轴为![]() ,故
,故![]() ;
;
又![]() ,
,
∴![]() ,
,
∴函数![]() 的周期为
的周期为![]() .
.
作出函数![]() 在一个周期上的图象(如图所示).
在一个周期上的图象(如图所示).
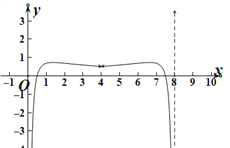
∵函数![]() 为偶函数,且不等式
为偶函数,且不等式![]() 在
在![]() 上有且只有200个整数解,
上有且只有200个整数解,
∴不等式在![]() 上有且只有100个整数解.
上有且只有100个整数解.
∵函数![]() 在
在![]() 内有25个周期,
内有25个周期,
∴函数![]() 在一个周期内有4个整数解,即
在一个周期内有4个整数解,即![]() 在
在![]() 内有4个整数解.
内有4个整数解.
①当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
由图象可得![]() 在一个周期内有7个整数解,不合题意.
在一个周期内有7个整数解,不合题意.
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
显然,![]() 在
在![]() 上无整数解,
上无整数解,
∴![]() 在
在![]() 上有4个整数解.
上有4个整数解.
∵![]() 的图象在
的图象在![]() 上关于
上关于![]() 对称,
对称,
∴![]() 在
在![]() 上有2个整数解.
上有2个整数解.
又![]() ,
,
∴![]() ,解得
,解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目