题目内容
如图,已知圆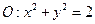 交
交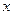 轴于
轴于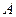 、
、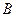 两点,
两点,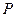 在圆
在圆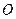 上运动(不与
上运动(不与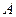 、
、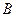 重合),过
重合),过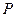 作直线
作直线 ,
,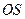 垂直于
垂直于 交直线
交直线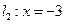 于点
于点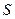 .
.
(1)求证:“如果直线 过点
过点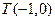 ,那么
,那么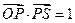 ”为真命题;
”为真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.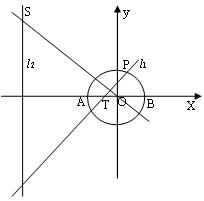
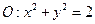 交
交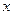 轴于
轴于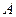 、
、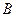 两点,
两点,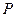 在圆
在圆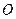 上运动(不与
上运动(不与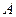 、
、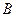 重合),过
重合),过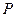 作直线
作直线 ,
,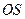 垂直于
垂直于 交直线
交直线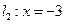 于点
于点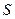 .
.(1)求证:“如果直线
 过点
过点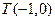 ,那么
,那么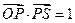 ”为真命题;
”为真命题;(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.

(1)证明见解析。
(2)逆命题为:如果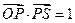 ,那么直线
,那么直线 过点
过点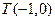 .逆命题也为真命题,
.逆命题也为真命题,
(2)逆命题为:如果
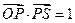 ,那么直线
,那么直线 过点
过点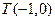 .逆命题也为真命题,
.逆命题也为真命题,(1)设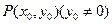 ,则
,则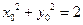 .当
.当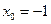 时,
时,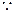 直线
直线 过点
过点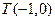 ,
, ,即
,即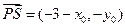 ,
,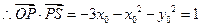 .当
.当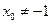 时,
时,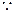 直线
直线 过点
过点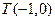 ,
,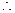 直线
直线 的斜率
的斜率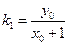 ,
,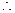 直线OS的斜率
直线OS的斜率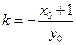 ,其方程为
,其方程为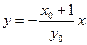 ,
,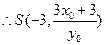 ,即
,即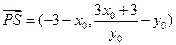 .
.
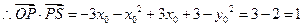 .故“如果直线
.故“如果直线 过点
过点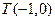 ,那么
,那么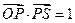 ”为真命题.
”为真命题.
(2)逆命题为:如果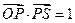 ,那么直线
,那么直线 过点
过点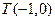 .逆命题也为真命题,以下给出证明:设
.逆命题也为真命题,以下给出证明:设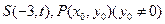 ,则
,则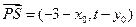 ,
, ,
,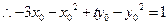 ,又
,又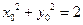 ,
,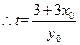 .当
.当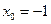 时,直线
时,直线 的方程为
的方程为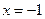 ,显然过点
,显然过点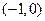 ;当
;当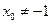 时,直线OS的斜率
时,直线OS的斜率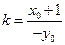 ,
,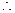 直线
直线 的方程为
的方程为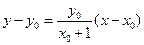 ,令
,令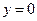 ,得
,得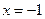 ,
,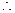 直线
直线 过定点
过定点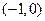 .综上,直线
.综上,直线 恒过定点
恒过定点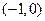 .
.
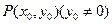 ,则
,则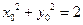 .当
.当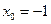 时,
时,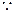 直线
直线 过点
过点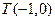 ,
, ,即
,即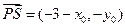 ,
,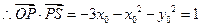 .当
.当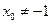 时,
时, 直线
直线 过点
过点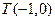 ,
, 直线
直线 的斜率
的斜率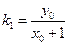 ,
,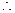 直线OS的斜率
直线OS的斜率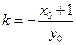 ,其方程为
,其方程为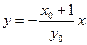 ,
,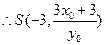 ,即
,即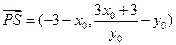 .
.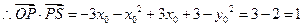 .故“如果直线
.故“如果直线 过点
过点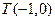 ,那么
,那么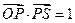 ”为真命题.
”为真命题.(2)逆命题为:如果
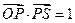 ,那么直线
,那么直线 过点
过点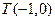 .逆命题也为真命题,以下给出证明:设
.逆命题也为真命题,以下给出证明:设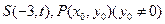 ,则
,则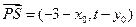 ,
, ,
,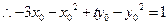 ,又
,又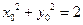 ,
,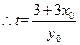 .当
.当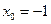 时,直线
时,直线 的方程为
的方程为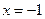 ,显然过点
,显然过点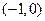 ;当
;当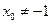 时,直线OS的斜率
时,直线OS的斜率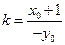 ,
, 直线
直线 的方程为
的方程为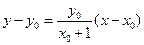 ,令
,令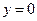 ,得
,得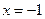 ,
, 直线
直线 过定点
过定点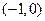 .综上,直线
.综上,直线 恒过定点
恒过定点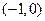 .
.
练习册系列答案
相关题目
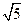 的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是
的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是



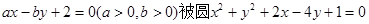 截得的弦长为4,则
截得的弦长为4,则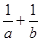 最小值是 ( )
最小值是 ( )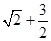


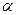 的直线交单位圆于点
的直线交单位圆于点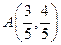 ,C是单位圆与
,C是单位圆与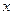 轴正半轴的交点,B是单位圆上第二象限的点,且
轴正半轴的交点,B是单位圆上第二象限的点,且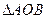 为正三角形。
为正三角形。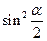 的值;
的值;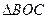 的面积。
的面积。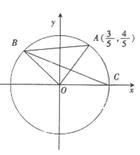
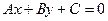 (其中
(其中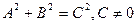 )与圆
)与圆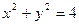 交于
交于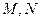 ,O是坐标原点,则
,O是坐标原点,则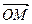 ·
·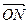 =( )
=( )  - 2
- 2  - 1
- 1  1
1  2
2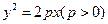 的准线与圆
的准线与圆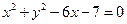 相切,则p的值为【】
相切,则p的值为【】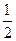
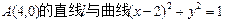 有公共点,则直线l的斜率的取值范围为________.
有公共点,则直线l的斜率的取值范围为________. 与圆
与圆 交于
交于 两点,则当
两点,则当 的面积最大时,
的面积最大时, _______
_______