题目内容
已知函数 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值所组成的集合A;
(Ⅱ)设关于x的方程 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式 对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?
【答案】
解:(Ⅰ) 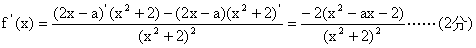
因为函数f(x)在区间[-1,1]上是增函数,所以f‘(x)≥0在区间x∈[-1,1]恒成立
即有x2-ax-2≤0在区间[-1,1]上恒成立。 构造函数g(x)=x2-ax-2
∴满足题意的充要条件是: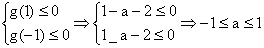
所以所求的集合A=[-1,1] ………(7分)
(Ⅱ)由题意得: 得到:x2-ax-2=0………(8分)
得到:x2-ax-2=0………(8分)
因为△=a2+8>0 所以方程恒有两个不等的根为x1、x2由根与系数的关系有:
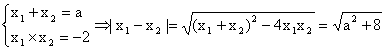 ……(9分)
……(9分)
因为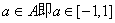 ,
,
所以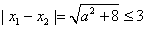 要使不等式
要使不等式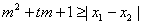
对任意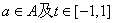 恒成立,
恒成立,
当且仅当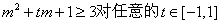 恒成立 ………………11分
恒成立 ………………11分
构造函数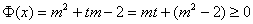
对任意的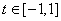 恒成立的充要条件是
恒成立的充要条件是
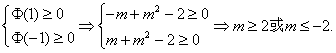
故存在实数m满足题意且为
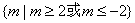 为所求。 ………………14分
为所求。 ………………14分

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
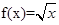 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.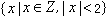 的非空真子集的个数是7;
的非空真子集的个数是7;
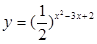 的单调递减区间是
的单调递减区间是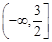 ;
; )=x+3,则
)=x+3,则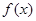 =
=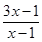 。
。