题目内容
已知向量 =(
=( sin2x,-f(x)),
sin2x,-f(x)), =(-m,cos2x+m-
=(-m,cos2x+m- )(m∈R) 且
)(m∈R) 且 与
与 互为相反向量.
互为相反向量.
(1)求f(x)的表达式;
(2)若x∈[0, ),f2(x)-λf(x)+1的最小值为-2,求实数λ的值.
),f2(x)-λf(x)+1的最小值为-2,求实数λ的值.
解:(1)由 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,
,
∴f(x)=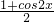 +
+ sin2x-
sin2x- =sin(2x+
=sin(2x+ ).
).
(2)∵x∈[0, ),∴2x+
),∴2x+ ∈[
∈[ ,
, ),∴
),∴ ≤sin(2x+
≤sin(2x+ )≤1,即f(x)∈[
)≤1,即f(x)∈[ ,1].
,1].
令 h=f2(x)-λf(x)+1,当 <
< 时,则h在[
时,则h在[ ,1]上是增函数,则f(x)=
,1]上是增函数,则f(x)= 时,h取得最小值为-2,
时,h取得最小值为-2,
故 -
- λ+1=-2,解得 λ=
λ+1=-2,解得 λ= (舍去).
(舍去).
当 ≤
≤ ≤1时,f(x)=
≤1时,f(x)= 时,h取得最小值为-2,即
时,h取得最小值为-2,即 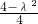 =-2,解得λ=±2
=-2,解得λ=±2 (舍去).
(舍去).
当 >1时,h在[
>1时,h在[ ,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4.
,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4.
综上可得,λ=4.
分析:(1)由 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,化简可得f(x)的解析式.
,化简可得f(x)的解析式.
(2)根据x∈[0, ),可得f(x)∈[
),可得f(x)∈[ ,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.
,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.
点评:本题主要考查两角和差的正弦公式,二倍角的余弦公式,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于中档题.
 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,
,∴f(x)=
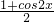 +
+ sin2x-
sin2x- =sin(2x+
=sin(2x+ ).
).(2)∵x∈[0,
 ),∴2x+
),∴2x+ ∈[
∈[ ,
, ),∴
),∴ ≤sin(2x+
≤sin(2x+ )≤1,即f(x)∈[
)≤1,即f(x)∈[ ,1].
,1].令 h=f2(x)-λf(x)+1,当
 <
< 时,则h在[
时,则h在[ ,1]上是增函数,则f(x)=
,1]上是增函数,则f(x)= 时,h取得最小值为-2,
时,h取得最小值为-2,故
 -
- λ+1=-2,解得 λ=
λ+1=-2,解得 λ= (舍去).
(舍去).当
 ≤
≤ ≤1时,f(x)=
≤1时,f(x)= 时,h取得最小值为-2,即
时,h取得最小值为-2,即 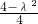 =-2,解得λ=±2
=-2,解得λ=±2 (舍去).
(舍去).当
 >1时,h在[
>1时,h在[ ,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4.
,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4.综上可得,λ=4.
分析:(1)由
 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,化简可得f(x)的解析式.
,化简可得f(x)的解析式.(2)根据x∈[0,
 ),可得f(x)∈[
),可得f(x)∈[ ,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.
,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.点评:本题主要考查两角和差的正弦公式,二倍角的余弦公式,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目