题目内容
若?x∈(1,5),使不等式x2-mx+4>0成立,则m的取值范围是________.
(-∞,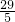 )
)
分析:分离变量可得所以m<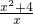 ,因为?x∈(1,5),使得m<
,因为?x∈(1,5),使得m<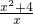 成立,只需m小于f(x)的最大值,然后构造函数,由导数求其单调性,可得取值范围.
成立,只需m小于f(x)的最大值,然后构造函数,由导数求其单调性,可得取值范围.
解答:不等式x2-mx+4>0可化为mx<x2+4,因为?x∈(1,5),所以m<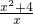
记函数f(x)=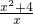 =
= ,x∈(1,5)只需m小于f(x)的最大值,
,x∈(1,5)只需m小于f(x)的最大值,
由f′(x)=1- =0可得x=2,而且当x∈(1,2)时,f′(x)<0,f(x)单调递减,
=0可得x=2,而且当x∈(1,2)时,f′(x)<0,f(x)单调递减,
当x∈(2,5)时,f′(x)>0,f(x)单调递增,
故最大值会小于f(1)或f(5),f(1)=5,f(5)=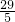
故只需m<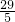 .
.
故答案为:(-∞,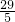 )
)
点评:本题为参数范围的求解,构造函数利用导数工具求取值范围是解决问题的工关键,本题要和恒成立区分,易错求成函数的最小值.
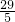 )
)分析:分离变量可得所以m<
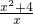 ,因为?x∈(1,5),使得m<
,因为?x∈(1,5),使得m<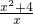 成立,只需m小于f(x)的最大值,然后构造函数,由导数求其单调性,可得取值范围.
成立,只需m小于f(x)的最大值,然后构造函数,由导数求其单调性,可得取值范围.解答:不等式x2-mx+4>0可化为mx<x2+4,因为?x∈(1,5),所以m<
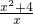
记函数f(x)=
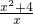 =
= ,x∈(1,5)只需m小于f(x)的最大值,
,x∈(1,5)只需m小于f(x)的最大值,由f′(x)=1-
 =0可得x=2,而且当x∈(1,2)时,f′(x)<0,f(x)单调递减,
=0可得x=2,而且当x∈(1,2)时,f′(x)<0,f(x)单调递减,当x∈(2,5)时,f′(x)>0,f(x)单调递增,
故最大值会小于f(1)或f(5),f(1)=5,f(5)=
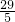
故只需m<
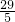 .
.故答案为:(-∞,
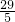 )
)点评:本题为参数范围的求解,构造函数利用导数工具求取值范围是解决问题的工关键,本题要和恒成立区分,易错求成函数的最小值.

练习册系列答案
相关题目