题目内容
已知x2+y2=10,则3x+4y的最大值为( )
分析:令z=3x+4y,可得直线y=-
x+
在y轴上的截距为
,当直线和圆x2+y2=10相切时,
取得最值,z取得最值.根据直线和圆相切,圆心到直线的距离等于半径,求出z的值,从而得到z的最大值.
| 3 |
| 4 |
| z |
| 4 |
| z |
| 4 |
| z |
| 4 |
解答:解:令z=3x+4y,即y=-
x+
,故直线y=-
x+
在y轴上的截距为
,
故当直线y=-
x+
在y轴上的截距最大时,z最大.
根据题意可得,当直线和圆x2+y2=10相切时,
取得最值.
由
=
可得z=±5
,故z的最大值为5
,
故选A.
| 3 |
| 4 |
| z |
| 4 |
| 3 |
| 4 |
| z |
| 4 |
| z |
| 4 |
故当直线y=-
| 3 |
| 4 |
| z |
| 4 |
根据题意可得,当直线和圆x2+y2=10相切时,
| z |
| 4 |
由
| 10 |
| |0+0-z| |
| 5 |
| 10 |
| 10 |
故选A.
点评:本题主要考查简单的线性规划问题,直线和圆相切的性质,点到直线的距离公式的应用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
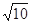 B 4
B 4