题目内容
椭圆中有如下结论：椭圆
上斜率为1的弦的中点在直线
上，类比上述结论：双曲线
上斜率为1的弦的中点在直线 上
解析试题分析：将椭圆方程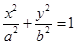
中的
变为
，
变为
，右边变为0，于此得到椭圆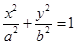上斜率为1的弦的中点在直线
上.
类比上述结论，将双曲线的方程作为上述变换可知：双曲线
上斜率为1的弦的中点在直线
.
不妨设弦的两个端点为
，
，则
，中点设为
，则
，
，将上述两端点代入双曲线方程得
，
两式相减得
，而
，
∴
，化简得
，
而
，
，于是在直线上.
考点：1.类比的思想；2.新定义题.
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
是椭圆
的半焦距，则
的取值范围为 .
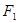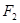的焦点
、
，点
为其上的动点，当∠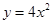
上的一点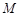
到焦点的距离为1，则点
的两焦点，过点F2的直线交椭圆于A，B两点．在
-
=1的右支上,若点A到右焦点的距离等于2x0,则x0= .
+
=1(a>b>0)的右顶点为A(1,0),过其焦点且垂直长轴的弦长为1,则椭圆方程为 .