Question

已知函数f(x)=ax³+bx²+cx(其中a≠0),且f′(-2)=0.

(1)若f(x)在x=2处取得极小值-2，求f(x)的单调区间；

(2)令F(x)=f′(x),若F′(x)＞0的解集是A，且A∪(0，1)=(-∞，1)，求的最大值.

Answer 1

解:(1)∵f′(x)=ax²+2bx+c,∴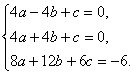

解得b=0,a=,c=.

∴f′(x)=x²≥0,得x≥2或x≤-2.

同理f′(x)=x²≤0,得-2≤x≤2.

即函数f(x)的单调减区间是［－2，2］，增区间是(-∞,-2］和［2,+∞).

(2)∵f′(x)=ax²+2bx+c=F(x),F(-2)=4a-4b+c=0,∴4b=4a+c.

F′(x)=2ax+2b=2ax+＞0,∴2ax＞.

当a＞0时，F′(x)＞0的解集是(,+∞),显然不满足A∪(0,1)=(-∞,1),

当a＜0时，F′(x)＞0的解集是(-∞,),

若满足A∪(0,1)=(-∞,1),则0＜≤1,

解得＜≤.∴的最大值为.