题目内容
20.设函数f(x)=|x+2|+|x-2|,x∈R,不等式f(x)≤6的解集为M.(1)求M;
(2)当a,b∈M时,证明:3|a+b|≤|ab+9|.
分析 (1)由条件利用绝对值的意义求出不等式f(x)≤6的解集M.
(2)用分析法证明此不等式,分析使此不等式成立的充分条件为(a2-9)(9-b2)≤0,而由条件a,b∈M可得(a2-9)(9-b2)≤0成立,从而证得要证的不等式.
解答 解:(1)不等式即|x+2|+|x-2|≤6,
而|x+2|+|x-2|表示数轴上的x对应点到-2、2对应点的距离之和,
-3和3对应点到-2、2对应点的距离之和正好等于6,
故不等式的解集为M=[-3,3].
(2)要证3|a+b|≤|ab+9|,只要证9(a+b)2≤(ab+9)2,
即证:9(a+b)2-(ab+9)2=9(a2+b2+2ab)-(a2•b2+18ab+81)=9a2+9b2-a2•b2-81=(a2-9)(9-b2)≤0,
而由a,b∈M,可得-3≤a≤3,-3≤b≤3,
∴(a2-9)≤0,(9-b2)≥0,∴(a2-9)(9-b2)≤0成立,
故要证的不等式3|a+b|≤|ab+9|成立.
点评 本题主要考查绝对值的意义、绝对值不等式的解法,用分析法证明不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
9.下列函数中,在(-1,1)内有零点且单调递增的是( )
| A. | y=log2(x+2) | B. | y=2x-1 | C. | y=x2-$\frac{1}{2}$ | D. | y=-x3 |
 如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.
如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB. 四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.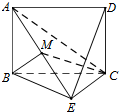 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.