题目内容
已知f(x)=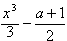 x2+ax+c(a≠1)。
x2+ax+c(a≠1)。
(1)讨论f(x)的单调性;
(2)当a=2时,已知f(x)的图象与x轴有三个不同的交点,求c的取值范围。
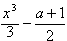 x2+ax+c(a≠1)。
x2+ax+c(a≠1)。(1)讨论f(x)的单调性;
(2)当a=2时,已知f(x)的图象与x轴有三个不同的交点,求c的取值范围。
解:(1)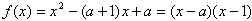
令f'(x)=0,得x=a或x=1
①当a<1时,在(-∞,a)、(1,+∞)上,f'(x)>0,
∴f(x)在(-∞,a)、(1,+∞)上单调递增;
在(a,1)上,f'(x)<0,
∴f(x)在(a,1)上单调递减;
②当a>1时,在(-∞,1)、(a,+∞)上,f'(x)>0,
∴f(x)在(-∞,1)、(a,+∞)上单调递增;
在(1,a)上,f'(x)<0,
∴f(x)在(1,a)上单调递减。
(2)当a=2时,由(1)知f(x)在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减
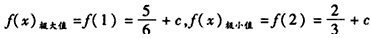
要使f(x)的图象与x轴有三个不同的交点,则需满足
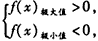 即
即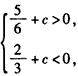
解得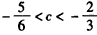 。
。
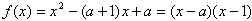
令f'(x)=0,得x=a或x=1
①当a<1时,在(-∞,a)、(1,+∞)上,f'(x)>0,
∴f(x)在(-∞,a)、(1,+∞)上单调递增;
在(a,1)上,f'(x)<0,
∴f(x)在(a,1)上单调递减;
②当a>1时,在(-∞,1)、(a,+∞)上,f'(x)>0,
∴f(x)在(-∞,1)、(a,+∞)上单调递增;
在(1,a)上,f'(x)<0,
∴f(x)在(1,a)上单调递减。
(2)当a=2时,由(1)知f(x)在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减
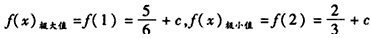
要使f(x)的图象与x轴有三个不同的交点,则需满足
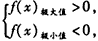 即
即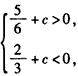
解得
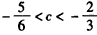 。
。
练习册系列答案
相关题目