题目内容
已知函数f(x)＝
，
(1)判断函数f(x)在区间(0，＋∞)上的单调性并加以证明；
(2)求函数f(x)的值域.
(1)当x>0时，f(x)＝＝
＝1－
.
设0<x1<x2，f(x1)－f(x2)＝(1－
)－(1－
)＝
，
由0<x1<x2可得f(x1)－f
(x2)<0，
即f(x1)<f(x2)，
因此f(x)在(0，＋∞)上递增.
(2)f(x)＝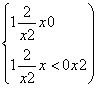
.
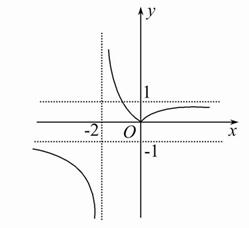
可以证明f(x)在(－∞，－2)上递减，且f(x)在(－2,0)上递减，由反比例函数y＝
通过平移、对称变换得f(x)的图象如图所示，因此f(x)的值域为：(－∞，－1)∪[0，＋∞).
练习册系列答案
相关题目
)x有两个零点x1，x2，则有