题目内容
（本小题13分）已知关于x的一元二次函数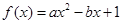
，分别从集合P和Q中随机取一个数a和b得到数列
。
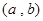（1）若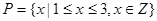
，
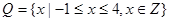，列举出所有的数对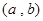，并求函数
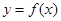有零点的概率；
（2）若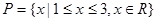
，
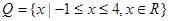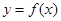，求函数在区间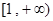
上是增函数的概率。
(1) 
(2) 
解析试题分析：（1）由已知得， 
所有的有序数列有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共有18对
要使
有零点 
满足条件的有序数对有，，，，，共有6对
（2）要使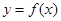单调递增，
即
可看成是平面区域
中的所有点
而满足条件是在平面区域
中的所有点
考点：古典概型和几何概型
点评：解决的关键是利用概型的区别合理的适用概率公式求解概率值，属于基础题。
练习册系列答案
相关题目
,且每个问题回答正确与否相互独立.
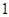次，求在这一枪出现空弹的概率；
次，求在这三枪中出现空弹的概率；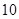 
的等边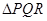
，甲射手用实弹瞄准了三角形
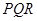区域随机射击，且弹孔都落在三角形
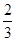，服用B有效的概率为
。
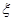表示这3个试验组中甲类组的个数，求
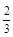，且每题正确完成与否互不影响。
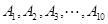等10所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为
.
元，该同学决定按
的分布列及数学期望.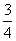
，乙答对每个题的概率为
。
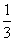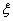，求