题目内容
(2005
全国Ⅱ,22)已知a≥0,函数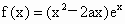 .
.
(1)
当x为何值时,f(x)取得最小值?证明你的结论;(2)
设f(x)在[-1,1]上是单调函数,求a的取值范围.
答案:略
解析:
提示:
解析:
|
解析: (1)对函数f(x)求导数,得
令  ,得 ,得 , ,
从而  . .
解得  , , , ,
其中  .当x变化时, .当x变化时, 、f(x)的变化如下表: 、f(x)的变化如下表:
即 f(x)在 处取到极大值,在 处取到极大值,在 处取到极小值. 处取到极小值.
当 a 0时, 0时, , , ,f(x)在 ,f(x)在 上为减函数,在 上为减函数,在 上为增函数. 上为增函数.
而当 x<0时, ,当x=0时,f(x)=0. ,当x=0时,f(x)=0.
所以当  时,f(x)取得最小值. 时,f(x)取得最小值.
(2) 当a≥0时,f(x)在[-1,1]上为单调函数的充要条件是 ,即 ,即 ,解得 ,解得 . .
综上, f(x)在[-1,1]上为单调函数的充分必要条件为 ,即a的取值范围是 ,即a的取值范围是 . . |
提示:
|
剖析:本题考查函数求导,函数的单调性及函数的最值问题. |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目


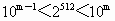 ,则m=_______(lg 2≈0.3010).
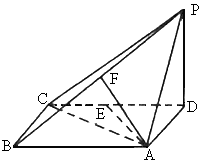
,则m=_______(lg 2≈0.3010).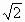 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.