题目内容
13.求垂直于直线2x-6y+1=0并且与曲线f(x)=x3+3x2-5相切的直线方程.分析 欲求切线方程,只须求出切点坐标即可,设切点为P(a,b),先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率列出等式求出a,b值.从而问题解决.
解答 解:设切点为P(a,b),函数y=x3+3x2-5的导数为y′=3x2+6x
切线的斜率k=y′|x=a=3a2+6a=-3,得a=-1,代入到y=x3+3x2-5,
得b=-3,即P(-1,-3),y+3=-3(x+1),
即直线方程为:3x+y+6=0.
点评 本小题主要考查互相垂直的直线的斜率间的关系、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
1.在平面直角坐标系中,直线l的参数方程是$\left\{\begin{array}{l}x=t\\ y=\sqrt{3}t\end{array}\right.$(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ-2ρsinθ-3=0.若直线l与曲线C相交于A、B两点,则|AB|=( )
| A. | $3\sqrt{5}$ | B. | $\sqrt{15}$ | C. | 3 | D. | $\sqrt{5}$ |
18.若数列{an}是等差数列,首项a2=37,a5=28,则Sn取最大值时,n=( )
| A. | 13 | B. | 14 | C. | 15 | D. | 14或15 |
3.设集合P={x|y=log2x},Q=|y|y=x3},则P∩Q等于( )
| A. | R | B. | [0,+∞) | C. | (0,+∞) | D. | [1,+∞) |
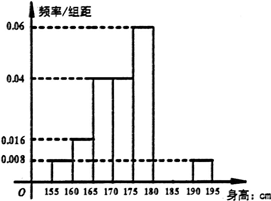 某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.
某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.