题目内容
函数 的值域为________.
的值域为________.
(-∞,-3]
分析:配方可得x2-4x+12≥8,由复合函数的单调性可知: ≤
≤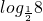 ,计算可得.
,计算可得.
解答:配方可得x2-4x+12=x2-4x+4+8=(x-2)2+8≥8,
由复合函数的单调性可知: ≤
≤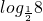 =-3,
=-3,
故函数的值域为(-∞,-3]
故答案为:(-∞,-3]
点评:本题考查函数的值域,涉及二次函数的值域的求解,和复合函数的单调性,属基础题.
分析:配方可得x2-4x+12≥8,由复合函数的单调性可知:
 ≤
≤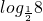 ,计算可得.
,计算可得.解答:配方可得x2-4x+12=x2-4x+4+8=(x-2)2+8≥8,
由复合函数的单调性可知:
 ≤
≤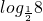 =-3,
=-3,故函数的值域为(-∞,-3]
故答案为:(-∞,-3]
点评:本题考查函数的值域,涉及二次函数的值域的求解,和复合函数的单调性,属基础题.

练习册系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: