Question

若等比数列{a_n}的前n项和S_n=2^n-1-c（c为常数），则c=________．

Answer 1

分析：先根据Sn与a_n的固有关系an=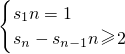，求出a₁，a₂，a₃，再由a₂²=a₁•a₃能够得到常数a的值．
解答：因为数列{a_n}的前n项和S_n=2^n-1_-c 所以S₁=1-c，S₂=2-c，S₃=4-c，
又因为a₁=s₁，a₂=s₂-s₁，a₃=s₃-s₂，所以a₁=1-c，a₂=1，a₃=2
根据数列{a_n}是等比数列，可知a₁a₃=a₂²，所以（1-c）×2=1，解得，c=．
故答案为：
点评：本题考查了数列中S_n与通项a_n的关系应用，等比数列的定义，考查转化、计算能力．