题目内容
若满足
，
，
的
恰有一解，则实数
的取值范围是 ．
.
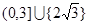解析试题分析：设
，则由余弦定理可得
，
∴满足条件的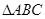
恰有一解，等价方程
仅有一正根，若
：则
符合题意；若
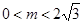：则方程必有一正根一非正根，∴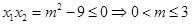
；
综上所述，满足条件的实数的取值范围是.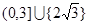
考点：解三角形与一元二次方程相结合.
练习册系列答案
相关题目
中，
（
分别为角
的对边），则
.
A=45°，C=60°,则BC= .
的中点，点D，E分别在半径OA，OB上．若
，则
的最大值是 .
中，已知
，则
.
中，角
的对边分别是
，若
，则
____.
则
.在
中，若
，则角B为（ ）
A． | B． | C． | D． |
题目内容
若满足，，的恰有一解，则实数的取值范围是 ．
.
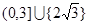解析试题分析：设，则由余弦定理可得，
∴满足条件的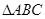恰有一解，等价方程仅有一正根，若：则符合题意；若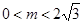：则方程必有一正根一非正根，∴；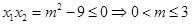
综上所述，满足条件的实数的取值范围是.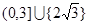
考点：解三角形与一元二次方程相结合.
在中，若，则角B为（ ）
| A． | B． | C． | D． |
，b，c，若
，b=2，sinB+cosB=
，
