Question

正方体ABCD-A₁B₁C₁D₁中，E，F分别是正方形ADD₁A₁和ABCD的中心，G是CC₁的中点，设GF，C₁E与AB所成的角分别为α，β，则α+β=

90°

．

Answer 1

分析：本题适合建立空间坐标系得用向量法解决这个立体几何问题，建立空间坐标系，给出有关点的坐标，求出直线的GF、C₁E与AB的方向向量，利用夹角公式求线线角的余弦值即可．

解答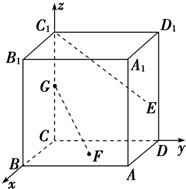：解：建立坐标系如图，
B（2，0，0），A（2，2，0），G（0，0，1），F（1，1，0），C₁（0，0，2），E（1，2，1）．
则

BA

=（0，2，0），

GF

=（1，1，-1），

C1E

=（1，2，-1），
∴cos＜

BA

，

GF

＞=

BA • GF

| BA |×|  GF |

=

2

2× 3

=

1

3

，
同理cos＜

BA

，

C1E

＞=

2

3

，
∴cosα=

1

3

，sinα=

2

3

，
cosβ=

2

3

，sinβ=

1

3

，
∴cos（α+β）=cosαcosβ-sinαsinβ=

1

3

•

2

3

-

2

3

•

1

3

=0
∴α+β=90°，
故答案为：90°．

点评：考查用空间向量为工具解决立体几何问题，此类题关键是找清楚线的方向向量，最后利用夹角公式计算．