题目内容
设函数f(x)满足x2f′(x)＋2xf(x)＝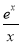
，f(2)＝
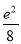，则x＞0时，f(x)( )．
A．有极大值，无极小值
B．有极小值，无极大值
C．既有极大值又有极小值
D．既无极大值也无极小值
D
【解析】由x2f′(x)＋2xf(x)＝
，得f′(x)＝
，令g(x)＝ex－2x2f(x)，x＞0，则g′(x)＝ex－2x2f′(x)－4xf(x)＝ex－2·
＝
.令g′(x)＝0，得x＝2.当x＞2时，g′(x)＞0；0＜x＜2时，g′(x)＜0，∴g(x)在x＝2时有最小值g(2)＝e2－8f(2)＝0，从而当x＞0时，f′(x)≥0，则f(x)在(0，＋∞)上是增函数，所以函数f(x)无极大值，也无极小值．
练习册系列答案
相关题目
