题目内容
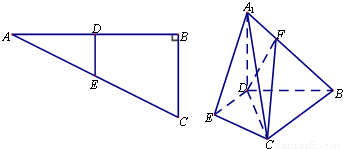
已知Rt△ABC中,![]() ,AB=1,BC=2,D为BC的中点,将△ADB沿AD折起,使点B在△ADC所在平面的射影E在AC上.
,AB=1,BC=2,D为BC的中点,将△ADB沿AD折起,使点B在△ADC所在平面的射影E在AC上.
(Ⅰ)求证:CD⊥平面BDE;
(Ⅱ)求折起后二面角BADC的大小;
(Ⅲ)求折起后AB与平面BDE所成的角.
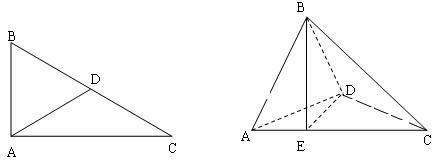
(Ⅰ)在对折图中作BO⊥AD于O,连结OE,由条件及三垂线定理知OE⊥AD,

对照原图知点B、O、E共线,∴在原图中
∵BA=BD,∴BE是AD中垂线,
∴∠BDE=∠BAE=900,∴CD⊥DE, 又∵BE⊥平面ACD, ∴CD⊥BE,∴CD⊥平面BDE
![]()
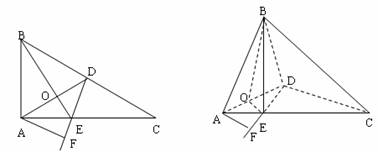
(Ⅱ):由(Ⅰ)知∠BOE就是二面角B-AD-C的平面角,
如原图,易求得BO=![]() ,OE=
,OE=![]() ,∴∠BOE= arccos
,∴∠BOE= arccos![]() ,
,
∴二面角B-AD-C的大小为arccos![]()
(Ⅲ):在对折图中作AF⊥ED于F,连结BF,由条件及知AF⊥平面BDE ,
∴∠ABF就是AB与平面BDE成的角,
如原图,易求得AF=![]() , ∴∠ABF=300
, ∴∠ABF=300
故AB与平面BDE所成的角为30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
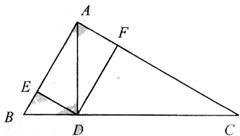 已知Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DF⊥AC,垂足为F,DE⊥AB,垂足为E.
已知Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DF⊥AC,垂足为F,DE⊥AB,垂足为E. 如图,已知Rt△ABC 中,AB=AC=
如图,已知Rt△ABC 中,AB=AC=

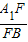 .
.