题目内容
数列{an }满足 ,
, .
.
(1)求数列{an}通项公式
(2)若 ,{bn}的前n次和为Bn,若存在整数m,对任意n∈N+且n≥2都有
,{bn}的前n次和为Bn,若存在整数m,对任意n∈N+且n≥2都有 成立,求m的最大值.
成立,求m的最大值.
解:(1)∵ ,
,
∴ =
= =-1+
=-1+
∴ -
- =-1
=-1
∵ ,∴
,∴
∴{ }是首项为-2,公差为-1的等差数列
}是首项为-2,公差为-1的等差数列
∴ =-2+(n-1)×(-1)=-(n+1)
=-2+(n-1)×(-1)=-(n+1)
∴ ;
;
(2)∵ ,∴
,∴ =
=
令Cn=B3n-Bn= +…+
+…+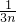
∴Cn+1-Cn=[ +…+
+…+ ]-(
]-( +…+
+…+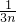 )=
)=
= >
> =0
=0
∴Cn+1-Cn>0,∴{Cn}为单调递增数列
∴(Cn)min=C2=B6-B2= =
=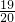
∴ ,∴m<19
,∴m<19
又m∈N+,
∴m的最大值为18.
分析:(1)利用数列递推式,可得{ }是首项为-2,公差为-1的等差数列,利用等差数列的求和公式,即可求得数列的通项;
}是首项为-2,公差为-1的等差数列,利用等差数列的求和公式,即可求得数列的通项;
(2)确定数列{bn}的通项,令Cn=B3n-Bn,确定其单调递增,求出最小值,从而可求m的最大值.
点评:本题考查数列递推式,考查数列的通项,考查数列的单调性,考查恒成立问题,确定数列的通项是关键.
 ,
,∴
 =
= =-1+
=-1+
∴
 -
- =-1
=-1∵
 ,∴
,∴
∴{
 }是首项为-2,公差为-1的等差数列
}是首项为-2,公差为-1的等差数列∴
 =-2+(n-1)×(-1)=-(n+1)
=-2+(n-1)×(-1)=-(n+1)∴
 ;
;(2)∵
 ,∴
,∴ =
=
令Cn=B3n-Bn=
 +…+
+…+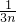
∴Cn+1-Cn=[
 +…+
+…+ ]-(
]-( +…+
+…+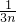 )=
)=
=
 >
> =0
=0∴Cn+1-Cn>0,∴{Cn}为单调递增数列
∴(Cn)min=C2=B6-B2=
 =
=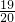
∴
 ,∴m<19
,∴m<19 又m∈N+,
∴m的最大值为18.
分析:(1)利用数列递推式,可得{
 }是首项为-2,公差为-1的等差数列,利用等差数列的求和公式,即可求得数列的通项;
}是首项为-2,公差为-1的等差数列,利用等差数列的求和公式,即可求得数列的通项;(2)确定数列{bn}的通项,令Cn=B3n-Bn,确定其单调递增,求出最小值,从而可求m的最大值.
点评:本题考查数列递推式,考查数列的通项,考查数列的单调性,考查恒成立问题,确定数列的通项是关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目