题目内容
已知函数 是R上的奇函数,
是R上的奇函数,
(1)求m的值;
(2)先判断f(x)的单调性,再证明之.
解:(1)因为函数 是R上的奇函数,故有f(0)=0,即m-
是R上的奇函数,故有f(0)=0,即m-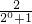 =0,
=0,
解得m=1.
(2)f(x)在R上单调递增,以下证明之:
任取x1,x2∈R,且x1<x2,则
∵ ,
,
∴f(x2)-f(x1)>0,所以f(x2)>f(x1),
故f(x)在R上单调递增.
分析:(1)特值法:利用R上的奇函数满足f(0)=0,即可求得m值.
(2)利用函数单调性的定义.
点评:本题考查了函数的奇偶性、单调性,准确理解相关定义是解决本题的基础.
 是R上的奇函数,故有f(0)=0,即m-
是R上的奇函数,故有f(0)=0,即m-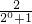 =0,
=0,解得m=1.
(2)f(x)在R上单调递增,以下证明之:
任取x1,x2∈R,且x1<x2,则

∵
 ,
,∴f(x2)-f(x1)>0,所以f(x2)>f(x1),
故f(x)在R上单调递增.
分析:(1)特值法:利用R上的奇函数满足f(0)=0,即可求得m值.
(2)利用函数单调性的定义.
点评:本题考查了函数的奇偶性、单调性,准确理解相关定义是解决本题的基础.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com] 且
且 ;
; 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则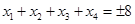 ;
; ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)