Question

某工厂有A，B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件耗时1 h，每生产一件乙产品使用4个B配件耗时2 h，该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天8 h计算，若生产一件甲产品获利2万元，生产一件乙产品获利3万元，问：如何安排生产才能使利润最大？

Answer 1

解析：设甲、乙两种产品分别生产x件、y件，工厂获得的利润为z，由已知条件可得二元一次不等式组：

目标函数为z＝2x＋3y.

把z＝2x＋3y变形为y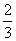＝－x＋，这是斜率为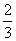－，在y轴上的截距为的直线．当z变化时，可以得到一组互相平行的直线，当截距最大时，z取得最大值．由上图可以看出，当直线y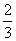＝－x＋过直线x＝4与直线x＋2y－8＝0的交点M(4,2)时，截距的值最大，最大值为，这时2x＋3y＝14.所以，每天生产甲产品4件，乙产品2件时，工厂可获得最大利润14万元．