题目内容
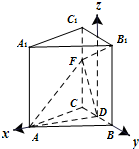
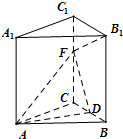 直三棱柱ABC-A1B1C1中AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
直三棱柱ABC-A1B1C1中AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
(1)求证:B1F⊥平面ADF;
(2)求平面ADF与平面AA1B1B所成锐二面角的余弦值.
(1)证明:以D为坐标原点,DA、DB、DD1分别为
x、y、z轴建立空间直角坐标系(D1是C1B1的中点),则A(2 a,0,0),B(0,a,0),F(0,-a,2a),B1(0,a,3a),(4分)
a,0,0),B(0,a,0),F(0,-a,2a),B1(0,a,3a),(4分)
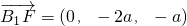 ,
,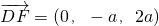 ,
,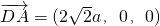 ,
,
由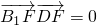 且
且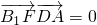 ,得B1F⊥DF,B1F⊥DA,
,得B1F⊥DF,B1F⊥DA,
∵DF∩DA=D
∴B1F⊥平面ADF;(6分)
(2)由(1)知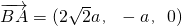 ,
,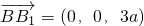 ,
,
设平面AA1B1B的一个法向量为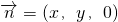 ,
,
则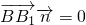 且
且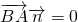 ,可取
,可取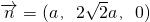 ,(8分)
,(8分)
由cos<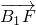 ,
, >=
>=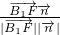 =-
=-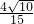
即所求二面角的余弦值是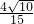 .(13分)
.(13分)
分析:(1)以D为坐标原点,DA、DB、DD1分别为x、y、z轴建立空间直角坐标系(D1是C1B1的中点),建立空间直角坐标系,用坐标表示点与向量,证明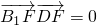 且
且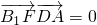 ,即可证得B1F⊥平面ADF;
,即可证得B1F⊥平面ADF;
(2)求得平面AA1B1B的一个法向量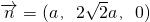 ,利用cos<
,利用cos<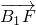 ,
, >=
>=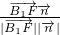 ,即可求得二面角的余弦值.
,即可求得二面角的余弦值.
点评:本题考查线面垂直,考查面面角,解题的关键是建立空间直角坐标系,利用向量方法解决立体几何问题,属于中档题.
x、y、z轴建立空间直角坐标系(D1是C1B1的中点),则A(2
 a,0,0),B(0,a,0),F(0,-a,2a),B1(0,a,3a),(4分)
a,0,0),B(0,a,0),F(0,-a,2a),B1(0,a,3a),(4分)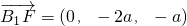 ,
,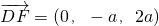 ,
,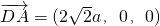 ,
,
由
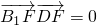 且
且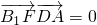 ,得B1F⊥DF,B1F⊥DA,
,得B1F⊥DF,B1F⊥DA,∵DF∩DA=D
∴B1F⊥平面ADF;(6分)
(2)由(1)知
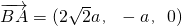 ,
,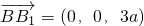 ,
,设平面AA1B1B的一个法向量为
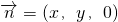 ,
,则
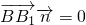 且
且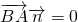 ,可取
,可取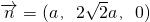 ,(8分)
,(8分)由cos<
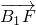 ,
, >=
>=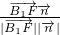 =-
=-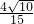
即所求二面角的余弦值是
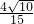 .(13分)
.(13分)分析:(1)以D为坐标原点,DA、DB、DD1分别为x、y、z轴建立空间直角坐标系(D1是C1B1的中点),建立空间直角坐标系,用坐标表示点与向量,证明
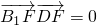 且
且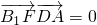 ,即可证得B1F⊥平面ADF;
,即可证得B1F⊥平面ADF;(2)求得平面AA1B1B的一个法向量
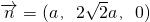 ,利用cos<
,利用cos<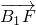 ,
, >=
>=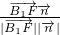 ,即可求得二面角的余弦值.
,即可求得二面角的余弦值.点评:本题考查线面垂直,考查面面角,解题的关键是建立空间直角坐标系,利用向量方法解决立体几何问题,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1= 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( ) 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







