题目内容
已知函数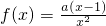 ,其中a>0.
,其中a>0.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(x)=xlnx-x2f(x),求g(x)在区间[1,e]上的最大值.(其中e为自然对数的底数)
解:(Ⅰ)∵函数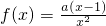 ,
,
∴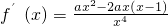 =
= ,
,
∵a>0,
∴由 >0,
>0,
得 ,或
,或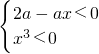 ,
,
∴0<x<2,或无解,
∴函数f(x)的单调增区间为(0,2).
由 <0,
<0,
得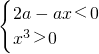 ,或
,或 ,
,
∴x>2或x<0.
∴函数f(x)的单调减区间为(-∞,0)和(2,+∞).
(Ⅱ)∵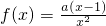 ,g(x)=xlnx-x2f(x),,
,g(x)=xlnx-x2f(x),,
∴g(x)=xlnx-a(x-1),
∴g'(x)=lnx+1-a,
当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);
当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;
当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).
设g(1)>g(e),即 e-a(e-1)<0,即 a>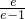 ,
,
所以若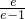 <a<2 时,最大值是g(1),
<a<2 时,最大值是g(1),
若1<a<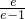 ,最大值是g(e).
,最大值是g(e).
综上,0<a<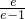 时,最大值是g(e)=e-a(e-1);
时,最大值是g(e)=e-a(e-1);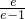 <a<2 时,最大值是g(1)=0.
<a<2 时,最大值是g(1)=0.
分析:(Ⅰ)由函数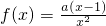 ,知
,知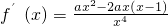 =
= ,由a>0,知当
,由a>0,知当 >0时,
>0时, ,或
,或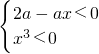 ,由此能求出函数f(x)的单调增区间;当
,由此能求出函数f(x)的单调增区间;当 <0时,
<0时,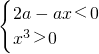 ,或
,或 ,由此能求出函数f(x)的单调减区间.
,由此能求出函数f(x)的单调减区间.
(Ⅱ)由g(x)=xlnx-a(x-1),知g'(x)=lnx+1-a,当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).由此能求出g(x)在区间[1,e]上的最大值.
点评:本题考查函数的单调区间的求法和求g(x)在区间[1,e]上的最大值.综合性强,难度大,是高考的重点.解题时要认真解答,注意导数性质的灵活运用.易错点是分类不清,导致出错.
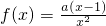 ,
,∴
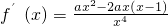 =
= ,
,∵a>0,
∴由
 >0,
>0,得
 ,或
,或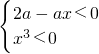 ,
,∴0<x<2,或无解,
∴函数f(x)的单调增区间为(0,2).
由
 <0,
<0,得
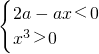 ,或
,或 ,
,∴x>2或x<0.
∴函数f(x)的单调减区间为(-∞,0)和(2,+∞).
(Ⅱ)∵
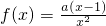 ,g(x)=xlnx-x2f(x),,
,g(x)=xlnx-x2f(x),,∴g(x)=xlnx-a(x-1),
∴g'(x)=lnx+1-a,
当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);
当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;
当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).
设g(1)>g(e),即 e-a(e-1)<0,即 a>
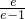 ,
,所以若
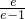 <a<2 时,最大值是g(1),
<a<2 时,最大值是g(1),若1<a<
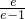 ,最大值是g(e).
,最大值是g(e).综上,0<a<
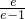 时,最大值是g(e)=e-a(e-1);
时,最大值是g(e)=e-a(e-1);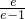 <a<2 时,最大值是g(1)=0.
<a<2 时,最大值是g(1)=0.分析:(Ⅰ)由函数
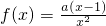 ,知
,知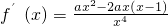 =
= ,由a>0,知当
,由a>0,知当 >0时,
>0时, ,或
,或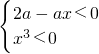 ,由此能求出函数f(x)的单调增区间;当
,由此能求出函数f(x)的单调增区间;当 <0时,
<0时,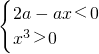 ,或
,或 ,由此能求出函数f(x)的单调减区间.
,由此能求出函数f(x)的单调减区间.(Ⅱ)由g(x)=xlnx-a(x-1),知g'(x)=lnx+1-a,当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).由此能求出g(x)在区间[1,e]上的最大值.
点评:本题考查函数的单调区间的求法和求g(x)在区间[1,e]上的最大值.综合性强,难度大,是高考的重点.解题时要认真解答,注意导数性质的灵活运用.易错点是分类不清,导致出错.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.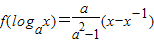 ,其中a>0且a≠1.
,其中a>0且a≠1.