题目内容
【题目】已知![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ;数列
;数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,问:数列
,问:数列![]() 中是否存在不同两项
中是否存在不同两项![]() ,
,![]() (
(![]() ,i,
,i,![]() ),使
),使![]() 仍是数列
仍是数列![]() 中的项?若存在,请求出i,j;若不存在,请说明理由.
中的项?若存在,请求出i,j;若不存在,请说明理由.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)存在,
,(3)存在,![]() ,
,![]()
【解析】
(1)先根据![]() ,求出
,求出![]() ,再根据
,再根据![]() 可得
可得![]() ,然后两式作差,得到
,然后两式作差,得到![]() ,再求出首项,进而可得数列
,再求出首项,进而可得数列![]() 的通项公式;
的通项公式;
(2)根据![]() ,通过递推,可证数列
,通过递推,可证数列![]() 为等差数列,即可求出通项公式;
为等差数列,即可求出通项公式;
(3)由![]() ,假设数列
,假设数列![]() 中存在不同两项
中存在不同两项![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ),然后根据条件找出满足条件的
),然后根据条件找出满足条件的![]() ,
,![]() 值即可.
值即可.
(1)∵数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]()
∴![]() ,
,![]()
由![]() ,得
,得![]() .
.
∴![]() ,且
,且![]() ,即
,即![]() .
.
∴数列![]() 是首项为
是首项为![]() ,公比为2的等比数列
,公比为2的等比数列
∴![]()
(2)∵![]() ①
①
![]() 时,
时,![]() ②
②
①![]() ②得
②得![]()
∴![]() ,
,![]()
![]() 时,
时,![]() ,∴
,∴![]()
∴![]()
∴![]() 为等差数列
为等差数列
∴![]()
(3)![]() ,假设
,假设![]() 中存在不同的两项
中存在不同的两项![]() ,
,![]() (
(![]() ),使
),使![]() (
(![]() )
)![]()
注意到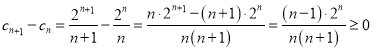 .
.
∴![]() 单调递增
单调递增
由![]() ,则
,则![]() .
.
∴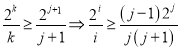
令![]() (
(![]() ),∴
),∴![]()
∴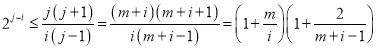
∵![]()
∴![]() ,而
,而![]()
∴![]() ,
,![]()
令![]() ,则
,则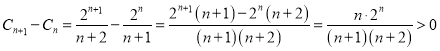
∴![]() 为单调递增,注意到
为单调递增,注意到![]() 时,
时,![]() ,
,![]()
∴m只能为1,2,3
①当![]() 时,
时,![]()
∴![]() ,故i只能为1,2,3
,故i只能为1,2,3
当![]() 时,
时,![]() ,此时
,此时![]()
当![]() 时,
时,![]() ,此时
,此时![]() 无整数解,舍
无整数解,舍
当![]() 时,
时,![]() ,此时
,此时![]() ,无正整数解,舍去
,无正整数解,舍去
②当![]() 时,
时,![]() ,此时
,此时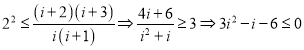
∴![]() ,此时
,此时![]() ,
,![]() 无解
无解
③当![]() 时,
时,![]() ,此时
,此时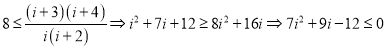 ,无正整数解,舍去.
,无正整数解,舍去.
综上:存在![]() ,
,![]() 满足题意.
满足题意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目