题目内容
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为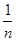
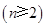 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如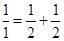 ,
,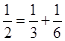 ,
,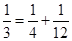 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )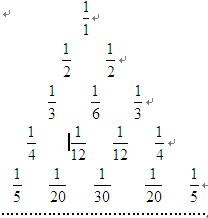
A.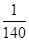 | B.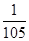 | C.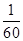 | D.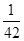 |
A
解析试题分析:记第n行的第m个数为 ,由题意知
,由题意知 ,
,
所以 ,
, ,
, ,
, ,
, ,因此选A。
,因此选A。
考点:归纳推理。
点评:本题考查通过观察归纳出各数的关系,考差了学生的观察能力和计算能力,属于中档题,解题时要认真审题,仔细解答,避免错误.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
若数列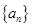 的前
的前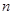 项和
项和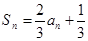 ,则数列
,则数列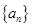 的通项公式
的通项公式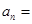 ( )
( )
A.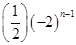 | B.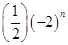 | C.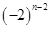 | D.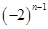 |
已知数列 为等差数列,
为等差数列,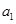 +
+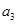 +
+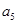
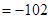 ,
,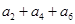
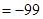 ,以
,以 表示
表示 的前
的前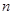 项和,则使得
项和,则使得 达到最小值的
达到最小值的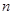 是( )
是( )
| A.37和38 | B.38 | C.37 | D.36和37 |
已知数列 成等差数列,
成等差数列,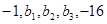 成等比数列,则
成等比数列,则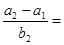 ( )
( )
A.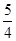 | B.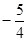 | C.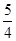 或 或 | D. |
一个赛跑机器人有如下特性:
(1)步长可以人为地设置成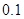 米,
米,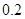 米,
米,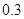 米,…,
米,…,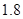 米或
米或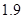 米;
米;
(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;
(3)当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒.
则这个机器人跑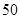 米(允许超出
米(允许超出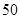 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.
A.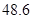 秒 秒 | B.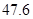 秒 秒 | C.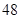 秒 秒 | D.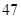 秒 秒 |
已知数列 满足:
满足: ,
, ,当且仅当
,当且仅当 时
时 最小,则实数
最小,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.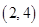 | D. |
数列 满足
满足 ,且对任意的
,且对任意的
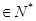 都有:
都有: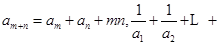
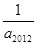 等于 ( )
等于 ( )
A. | B.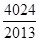 | C.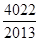 | D.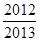 |
已知数列{an}的通项公式为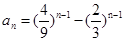 ,则数列{an}
,则数列{an}
| A.有最大项,没有最小项 | B.有最小项,没有最大项 |
| C.既有最大项又有最小项 | D.既没有最大项也没有最小项 |
 ).若数列{
).若数列{ }的前
}的前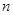 项和为
项和为 ,则
,则 = (用数字作答).
= (用数字作答).