题目内容
已知函数 是偶函数。
是偶函数。
(1)求 的值;
的值;
(2)设函数 ,其中实数
,其中实数 。若函数
。若函数 与
与 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数 的取值范围。
的取值范围。
 是偶函数。
是偶函数。(1)求
 的值;
的值;(2)设函数
 ,其中实数
,其中实数 。若函数
。若函数 与
与 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数 的取值范围。
的取值范围。(1)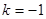 ;(2)
;(2)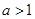
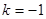 ;(2)
;(2)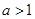
试题分析:(1)根据偶函数定义
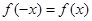 可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数
可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数 与
与 的图象有且只有一个交点的问题 为方程
的图象有且只有一个交点的问题 为方程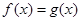 只有一个根的问题。将
只有一个根的问题。将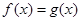 整理变形并结合换元法可转化为
整理变形并结合换元法可转化为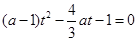 ,在
,在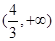 上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。
上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。试题解析:解:(1)∵
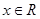 由题有
由题有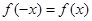 对
对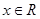 恒成立 …2分
恒成立 …2分即
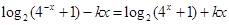 恒成立,整理得
恒成立,整理得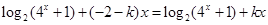 ,所以
,所以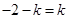 ∴
∴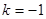
(2)由函数的定义域得
 , 由于
, 由于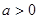
所以
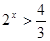 即定义域为
即定义域为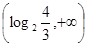
∵函数
 与
与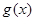 的图象有且只有一个交点,即方程
的图象有且只有一个交点,即方程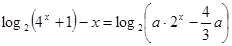 在
在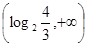 上只有一解。
上只有一解。即:方程
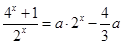 在
在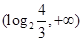 上只有一解
上只有一解令
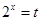 ,则
,则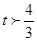 ,上式可变形为
,上式可变形为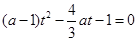 ,在
,在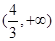 上只有一个解。
上只有一个解。当
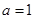 时,
时,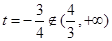 舍。
舍。当
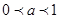 时,记
时,记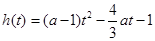 ,其图像的对称轴为
,其图像的对称轴为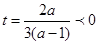 ,所以
,所以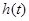 在
在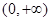 上单调递减,而
上单调递减,而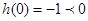 。所以方程
。所以方程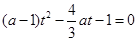 在
在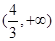 上无解。
上无解。当
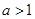 时,记
时,记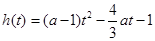 ,其图象的对称轴
,其图象的对称轴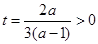
所以只需
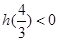 ,即
,即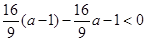 ,此恒成立
,此恒成立∴此时
 的范围为
的范围为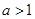
综上所述,所求
 的取值范围为
的取值范围为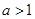

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
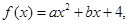 集合
集合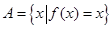
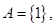 求函数
求函数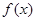 的解析式;
的解析式;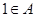 ,且
,且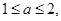 设
设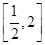 上的最大值、最小值分别为
上的最大值、最小值分别为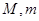 ,记
,记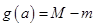 ,求
,求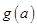 的最小值.
的最小值. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点 、
、 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为 .
. ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求 的取值范围.
的取值范围. ,例如:
,例如: ,
,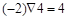 ,则函数
,则函数 的最大值为____________.
的最大值为____________.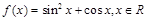 的最大值等于 .
的最大值等于 . (x
(x -2x+3)有以下4个结论:其中正确的有 .
-2x+3)有以下4个结论:其中正确的有 .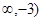
 ; ② 递增区间为
; ② 递增区间为 ;
; 轴的上方.
轴的上方.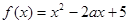 (
(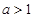 ),若
),若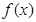 的定义域和值域均是
的定义域和值域均是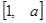 ,则实数
,则实数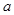 =
= 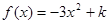 ,当实数
,当实数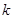 属于下列选项中的哪一个区间时,才能确保一定存在实数对
属于下列选项中的哪一个区间时,才能确保一定存在实数对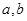 (
(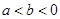 ),使得当函数
),使得当函数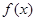 的定义域为
的定义域为 时,其值域也恰好是
时,其值域也恰好是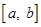 ( )
( )


