题目内容
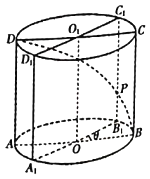
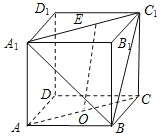
【题目】在正方体ABCD﹣A1B1C1D1中,O为线段AC的中点,点E在线段A1C1上,则直线OE与平面A1BC1所成角的正弦值的取值范围是( )
A.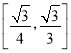 B.
B.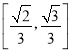 C.
C.![]() D.
D.![]()
【答案】B
【解析】
设正方体的边长为![]() ,以
,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,
,![]() ,则
,则![]() ,再求出平面A1BC1 的一个法向量,直线OE与平面A1BC1所成角为
,再求出平面A1BC1 的一个法向量,直线OE与平面A1BC1所成角为![]() ,利用空间向量的数量积,由
,利用空间向量的数量积,由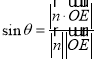 即可求解.
即可求解.
设正方体的边长为![]() ,以
,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴,
轴,
建立空间直角坐标系,如图所示:
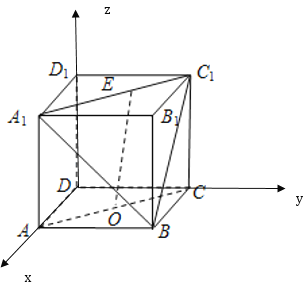
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
设平面A1BC1 的一个法向量为![]() ,
,
则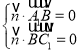 ,可得
,可得![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
设直线OE与平面A1BC1所成角为![]() ,
,
则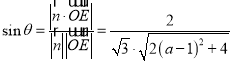 ,
,
当![]() 时,
时,![]() 取最大值为
取最大值为![]() ,
,
当![]() 或
或![]() 时,
时,![]() 取最小值为
取最小值为![]() ,
,
故直线OE与平面A1BC1所成角的正弦值的取值范围是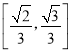 .
.
故选:B

 小学课时特训系列答案
小学课时特训系列答案【题目】鲤鱼是中国五千年文化传承的载体之一,它既是拼搏进取、敢于突破自我、敢于冒险奋进精神的载体,又是富裕、吉庆、幸运的美好象征.某水产养殖研究所为发扬传统文化,准备进行“中国红鯉”和“中华彩鲤”杂交育种实验.研究所对200尾中国红鲤和160尾中华彩鲤幼苗进行2个月培育后,将根据体长分别选择生长快的10尾中国红鲤和8尾中华彩鲤作为种鱼进一步培育.为了解培育2个月后全体幼鱼的体长情况,按照品种进行分层抽样,其中共抽取40尾中国红鲤的体长数据(单位:![]() )如下:
)如下:
5 | 6 | 7 | 7.5 | 8 | 8.4 | 4 | 3.5 | 4.5 | 4.3 |
5 | 4 | 3 | 2.5 | 4 | 1.6 | 6 | 6.5 | 5.5 | 5.7 |
3.1 | 5.2 | 4.4 | 5 | 6.4 | 3.5 | 7 | 4 | 3 | 3.4 |
6.9 | 4.8 | 5.6 | 5 | 5.6 | 6.5 | 3 | 6 | 7 | 6.6 |
(1)根据以上样本数据推断,若某尾中国红鲤的体长为![]() ,它能否被选为种鱼?说明理由;
,它能否被选为种鱼?说明理由;
(2)通过计算得到中国红鲤样本数据平均值为![]() ,中华彩鲤样本数据平均值为
,中华彩鲤样本数据平均值为![]() ,求所有样本数据的平均值;
,求所有样本数据的平均值;
(3)如果将8尾中华彩鲤种鱼随机两两组合,求体长最长的2尾组合到一起的概率.