Question

定义在R上的偶函数f（x），满足f(x+

1

2

)=-f(x+

3

2

)，且在区间[-1，0]上为递增，则（　　）

• A、f（3）＜f（

  2

  ）＜f（2）
• B、f（2）＜f（3）＜f（

  2

  ）
• C、f（3）＜f（2）＜f（

  2

  ）
• D、f（

  2

  ）＜f（2）＜f（3）

Answer 1

分析：由“f（x）是偶函数”和“f(x+

1

2

)=-f(x+

3

2

)”推出对称性：函数的图象关于x=1对称，再结合“在区间[-1，0]上为递增”知在“在区间[0，1]上为递减”作出一个函数图象，用数形结合法求解．

解答：解：∵f（x）是偶函数，
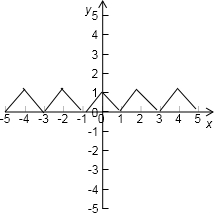
∴f（-x）=f（x）
∵f(x+

1

2

)=-f(x+

3

2

)，
∴f（x）=-f（x+1）
∴f（x）=f（2-x）
∴函数的图象关于x=1对称
∵在区间[-1，0]上为递增，
∴在区间[0，1]上为递减，
我们可以作出一个函数图象：
易得：f（3）＜f（

2

）＜f（2）
故选A

点评：本题主要考查函数的奇偶性，单调性，对称性和周期性，还考查了作图，用图能力，体现了数形结合的思想和方法．