题目内容
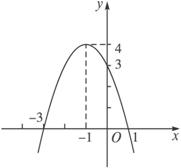
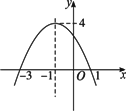
下图是一个二次函数y=f(x)的图象,试求这个函数的解析式.
答案:
解析:
提示:
解析:
|
解法一:设y=ax2+bx+c,然后把(-3,0)、(1,0)、(-1,4)代入解析式,得 解得a=-1,b=-2,c=3. ∴所求二次函数为y=-x2-2x+3. 解法二:∵二次函数与x轴有两个交点(-3,0)、(1,0),∴可设y=a(x+3)(x-1),再把(-1,4)代入,得2×(-2)×a=4. ∴a=-1. ∴所求二次函数为y=-(x+3)(x-1),即为y=-x2-2x+3. 解法三:∵抛物线的顶点为(-1,4),∴可设y=a(x+1)2+4,再把(1,0)代入得4a+4=0,a=-1. ∴所求二次函数为y=-(x+1)2+4,即为y=-x2-2x+3. 点评:二次函数解析式的设法有三种:一般式、顶点式、两根式,根据条件灵活选择. |
提示:
|
要确定二次函数的解析式,就是确定解析式中的待定系数(常数),由于每一种形式都含有三个待定系数,所以用待定系数法求二次函数解析式,需要已知三个独立的条件. |

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目

 有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.
有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.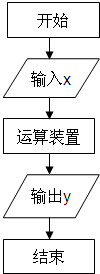 有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.
有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.