题目内容
(本小题满分12分)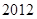 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行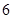 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午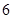 点到中午
点到中午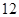 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出:
y=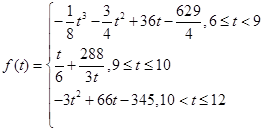
求从上午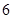 点到中午
点到中午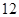 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。
上午 点。
点。
解析试题分析:当 时,
时,
得:
故: 在
在 单调递增,在
单调递增,在 单调递减,
单调递减,
因此,
 ;
;
当 时,
时, 。当且仅当
。当且仅当
即:
 。 因此
。 因此 在
在 单调递减,
单调递减,
所以, 。
。
当 时,
时, ,对称轴为
,对称轴为 ,
,
故 。
。
综上所述: 。
。
故:通过收费站用时最多的时刻为上午 点。
点。
考点:函数最值的实际应用;分段函数的最值求法;利用导数研究函数的单调性和最值;二次函数的性质;基本不等式。
点评:本题考查的知识点是函数的最值,分段函数的最值,导数求函数的最值,基本不等式求最值,难度较大.对于分段函数的最值我们要分段求,把各段的最值的都求出,再进行比较,最大的那个就是这个分段函数的最大值。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
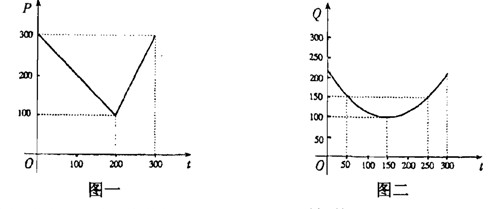
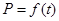 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式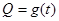 .
.
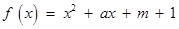 ,关于
,关于 的不等式
的不等式 的解集为
的解集为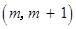 ,其中
,其中 为非零常数.设
为非零常数.设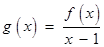 .
. 的值;
的值;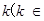 R
R 如何取值时,函数
如何取值时,函数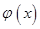
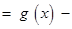
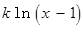 存在极值点,并求出极值点;
存在极值点,并求出极值点;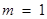 ,且
,且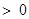 ,求证:
,求证: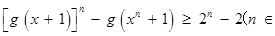 N
N
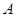 、
、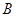 两个项目,预计投资
两个项目,预计投资 万元可获得利润
万元可获得利润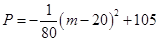
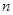 万元可获得利润
万元可获得利润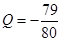
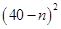
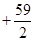
 万元.若该企业用40
万元.若该企业用40 ,设AB=2x,BC=y.
,设AB=2x,BC=y.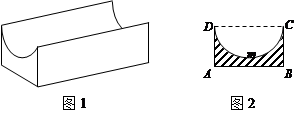
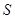 平方米.
平方米.
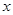 表示
表示 和用
和用 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为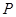 元,且
元,且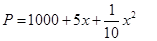 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为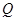 元,其中
元,其中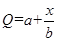
 ,
,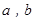 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本) , 求满足
, 求满足 的
的 的值。
的值。