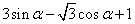题目内容
 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为2sinα-2cosα+2
2sinα-2cosα+2
.分析:根据正弦定理可先求出4个三角形的面积,再由余弦定理可求出正方形的边长进而得到面积,最后得到答案.
解答:解:由正弦定理可得4个等腰三角形的面积和为:4×
×1×1×sinα=2sinα.
由余弦定理可得正方形边长为:
=
,故正方形面积为:2-2cosα.
所以所求八边形的面积为:2sinα-2cosα+2,
故答案为:2sinα-2cosα+2.
| 1 |
| 2 |
由余弦定理可得正方形边长为:
| 12+12-2×1×1×cosα |
| 2-2cosα |
所以所求八边形的面积为:2sinα-2cosα+2,
故答案为:2sinα-2cosα+2.
点评:本题考查了三角面积公式的应用和余弦定理的应用,正、余弦定理是考查解三角形的重点,是必考内容.

练习册系列答案
相关题目
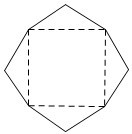 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为a的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为a的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )| A、2sinα-2cosα+2 | ||
B、sinα-
| ||
C、3sinα-
| ||
| D、2sinα-cosα+1 |
 的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积为
的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积为 B.
B.
 D.
D.
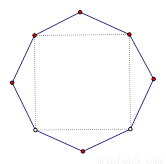
 的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )
的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )
 ; B.
; B.
 ; D.
; D.
 顶角为
顶角为 的四个等腰三角形,及其底边构成的正方形所
的四个等腰三角形,及其底边构成的正方形所 ;
;