题目内容
已知函数f(x)=log2(x+1),当点(x,y)是y=f(x)的图象上的点时,点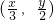 是y=g(x)的图象上的点.
是y=g(x)的图象上的点.
(I)写出y=g(x)的表达式;
(II)当g(x)-f(x)≥0时,求x的取值范围;
(Ⅲ)当x在(Ⅱ)所给范围取值时,求g(x)-f(x)的最大值.
解:(I)令 ,则x=3m,y=2n,由点(x,y)在y=log2(x+1)的图象上可得2n=log2(3m+1),故
,则x=3m,y=2n,由点(x,y)在y=log2(x+1)的图象上可得2n=log2(3m+1),故 ,
,
又(m,n)是函数y=g(x)的图象上的点,故 .
.
(II)因为g(x)-f(x)≥0,所以 .
.
由对数函数的性质可得 ,解得0≤x≤1.
,解得0≤x≤1.
(Ⅲ)因为0≤x≤1,
所以 .
.
当且仅当3x+1=2时,即 时等号成立,
时等号成立,
故g(x)-f(x)在[0,1]上的最大值为 .
.
分析:(I)令 ,由题设条件知
,由题设条件知 ,再由(m,n)是函数y=g(x)的图象上的点,可知
,再由(m,n)是函数y=g(x)的图象上的点,可知 .
.
(II)由题意知 .由对数函数的性质可得
.由对数函数的性质可得 ,解得0≤x≤1.
,解得0≤x≤1.
(Ⅲ)由题疫条件知 .由此可知g(x)-f(x)在[0,1]上的最大值为
.由此可知g(x)-f(x)在[0,1]上的最大值为 .
.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.
 ,则x=3m,y=2n,由点(x,y)在y=log2(x+1)的图象上可得2n=log2(3m+1),故
,则x=3m,y=2n,由点(x,y)在y=log2(x+1)的图象上可得2n=log2(3m+1),故 ,
,又(m,n)是函数y=g(x)的图象上的点,故
 .
.(II)因为g(x)-f(x)≥0,所以
 .
.由对数函数的性质可得
 ,解得0≤x≤1.
,解得0≤x≤1.(Ⅲ)因为0≤x≤1,
所以
 .
.当且仅当3x+1=2时,即
 时等号成立,
时等号成立,故g(x)-f(x)在[0,1]上的最大值为
 .
.分析:(I)令
 ,由题设条件知
,由题设条件知 ,再由(m,n)是函数y=g(x)的图象上的点,可知
,再由(m,n)是函数y=g(x)的图象上的点,可知 .
.(II)由题意知
 .由对数函数的性质可得
.由对数函数的性质可得 ,解得0≤x≤1.
,解得0≤x≤1.(Ⅲ)由题疫条件知
 .由此可知g(x)-f(x)在[0,1]上的最大值为
.由此可知g(x)-f(x)在[0,1]上的最大值为 .
.点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目