题目内容
已知a1=1,an=n(an+1-an)(n∈N*),则数列{an}的前60项和为________.
1830
分析:累乘法:由an=n(an+1-an),得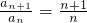 ,则
,则 ,代入数值即可求得an,注意验证a1是否满足.
,代入数值即可求得an,注意验证a1是否满足.
解答:由an=n(an+1-an),得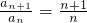 ,
,
所以,当n≥2时,累积得
=1× ×
× =n,
=n,
又a1也满足上式,故an=n,
所以数列{an}的前60项和为 .
.
故答案为:1830.
点评:本题考查数列的递推式及数列求和,若数列{an}满足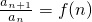 ,则往往运用累积法求an,注意验证a1.
,则往往运用累积法求an,注意验证a1.
分析:累乘法:由an=n(an+1-an),得
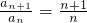 ,则
,则 ,代入数值即可求得an,注意验证a1是否满足.
,代入数值即可求得an,注意验证a1是否满足.解答:由an=n(an+1-an),得
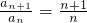 ,
,所以,当n≥2时,累积得

=1×
 ×
× =n,
=n,又a1也满足上式,故an=n,
所以数列{an}的前60项和为
 .
.故答案为:1830.
点评:本题考查数列的递推式及数列求和,若数列{an}满足
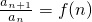 ,则往往运用累积法求an,注意验证a1.
,则往往运用累积法求an,注意验证a1. 
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目