题目内容
已知sin2α= ,
, .
.
(1)求cos2α及cosα的值;
(2)求满足条件sin(α-x)-sin(α+x)+2cosα=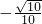 的锐角x.
的锐角x.
解:(1)因为 ,所以
,所以 .…(1分)
.…(1分)
因此cos2α=- =
= .…(4分)
.…(4分)
由cos2α=2cos2α-1,得cosα=- .…(7分)
.…(7分)
(2)因为sin(α-x)-sin(α+x)+2cosα=- ,
,
所以2cosα(1-sinx)=- ,所以sinx=
,所以sinx= .…(10分)
.…(10分)
因为x为锐角,所以x= .…(14分)
.…(14分)
分析:(1)利用α的范围,求出2α的范围,然后求出cos2α,通过二倍角公式求出cosα的值.
(2)通过已知表达式,求出sinx的值,推出结果即可.
点评:本题考查三角函数的化简求值,考查二倍角公式的应用,计算能力.
 ,所以
,所以 .…(1分)
.…(1分)因此cos2α=-
 =
= .…(4分)
.…(4分)由cos2α=2cos2α-1,得cosα=-
 .…(7分)
.…(7分)(2)因为sin(α-x)-sin(α+x)+2cosα=-
 ,
,所以2cosα(1-sinx)=-
 ,所以sinx=
,所以sinx= .…(10分)
.…(10分)因为x为锐角,所以x=
 .…(14分)
.…(14分)分析:(1)利用α的范围,求出2α的范围,然后求出cos2α,通过二倍角公式求出cosα的值.
(2)通过已知表达式,求出sinx的值,推出结果即可.
点评:本题考查三角函数的化简求值,考查二倍角公式的应用,计算能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知sin2α=-
,a∈(-
,0),则sinα+cosα=( )
| 24 |
| 25 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|