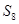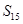题目内容
已知等差数列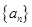 的前项和为
的前项和为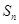 ,且
,且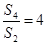 ,则
,则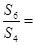 ( )
( )
A.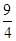 | B.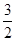 | C.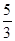 | D.4 |
A
解析试题分析:根据题意,由于等差数列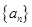 的前项和为
的前项和为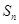 ,故根据其性质得到
,故根据其性质得到 构成了等差数列,则可知设
构成了等差数列,则可知设 ,可知
,可知 ,因此可知
,因此可知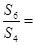
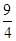 ,故选A.
,故选A.
考点:等差数列
点评:解题的关键是对于等差数列的等长连续片段的和构成的等差数列的运用,属于基础题。

练习册系列答案
相关题目
等差数列 前
前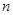 项和
项和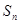 ,
,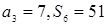 ,则公差d的值为 ( )
,则公差d的值为 ( )
| A.2 | B.3 | C.4 | D.-3 |
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |
如果等差数列 中,
中,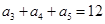 ,那么
,那么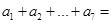 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
等差数列{an}和{bn}的前n项和分别为Sn和Tn,且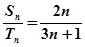 ,则
,则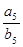 ( )
( )
A.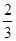 | B.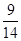 | C.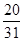 | D.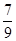 |
已知数列 满足
满足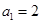 ,
,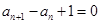
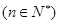 ,则此数列的通项
,则此数列的通项 等于( )
等于( )
A.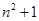 | B.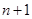 | C.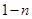 | D.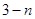 |
在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11=( )
| A.58 | B.88 | C.143 | D.176 |
若 为等差数列
为等差数列 的前n项和,
的前n项和, ,
,  ,则
,则 与
与 的等比中项为( )
的等比中项为( )
A. | B. | C. | D. |
 的公差为
的公差为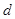 ,前
,前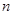 项和为
项和为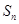 ,当首项
,当首项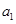 和
和 是一个定值,则下列各数中也为定值的是 ( )
是一个定值,则下列各数中也为定值的是 ( )