题目内容
定义在R上的偶函数f（x）的部分图象如图所示，则在（-2，0）上，下列函数中与f（x）的单调性不同的是（ ）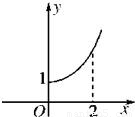
A．y=x2+1
B．y=|x|+1
C．y=
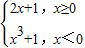
D．y=
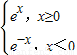
【答案】分析：首先利用偶函数的对称性，判断出f（x）在（-2，0）为减函数．然后分别对选项中4个函数分析单调性．最后判断答案即可．
解答：解：利用偶函数的对称性
知f（x）在（-2，0）上为减函数．
又y=x2+1在（-2，0）上为减函数；
y=|x|+1在（-2，0）上为减函数；
y=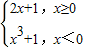
在（-2，0）上为增函数．
∴y=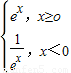
在（-2，0）上为减函数．
故选C．
点评：本题考查函数的奇偶性与单调性的关系，涉及到二次函数，绝对值函数，一次函数，3次函数，以及指数函数的单调性．属于中档题．
解答：解：利用偶函数的对称性
知f（x）在（-2，0）上为减函数．
又y=x2+1在（-2，0）上为减函数；
y=|x|+1在（-2，0）上为减函数；
y=
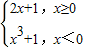在（-2，0）上为增函数．∴y=
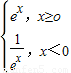在（-2，0）上为减函数．故选C．
点评：本题考查函数的奇偶性与单调性的关系，涉及到二次函数，绝对值函数，一次函数，3次函数，以及指数函数的单调性．属于中档题．
练习册系列答案
相关题目
已知定义在R上的偶函数f（x）．当x≥0时，