题目内容
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为 ,乙投篮命中的概率为
,乙投篮命中的概率为
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.
【答案】分析:(Ⅰ)甲至多命中2个且乙至少命中2个包含的两个事件是相互独立事件,分别做出甲至多命中2个球的概率和乙至少命中两个球的概率,根据相互独立事件的概率公式得到结果.
(II)乙所得分数为η,η可能的取值-4,0,4,8,12,当变量是-4时,表示一个球也没进,当变量是0时,表示只进一个球,当变量是4时,表示进了2个球,当变量是8时,表示进了3个球,当变量是12时,表示进了4个球,结合变量对应的事件和独立重复试验写出分布列和期望.
解答:解:(Ⅰ)甲至多命中2个且乙至少命中2个包含的两个事件是相互独立事件,
设“甲至多命中2个球”为事件A,“乙至少命中两个球”为事件B,由题意得: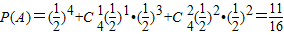
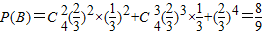
∴甲至多命中2个球且乙至少命中2个球的概率为:
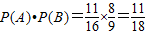
(Ⅱ)乙所得分数为η
η可能的取值-4,0,4,8,12,
P(η=-4)=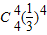 =
=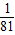 ,
,
P(η=0)=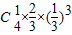 =
=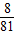
P(η=4)=C42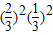 =
=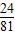
P(η=8)=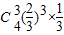 =
=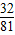
P(η=-4)=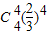 =
=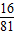
分布列如下:

∴Eη=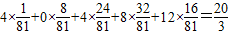 .
.
点评:本题考查独立重复试验,考查离散型随机变量的分布列和期望,是一个综合题,解题时注意进球的个数对应的是乙所得的分数,注意分数与进球个数的对应.
(II)乙所得分数为η,η可能的取值-4,0,4,8,12,当变量是-4时,表示一个球也没进,当变量是0时,表示只进一个球,当变量是4时,表示进了2个球,当变量是8时,表示进了3个球,当变量是12时,表示进了4个球,结合变量对应的事件和独立重复试验写出分布列和期望.
解答:解:(Ⅰ)甲至多命中2个且乙至少命中2个包含的两个事件是相互独立事件,
设“甲至多命中2个球”为事件A,“乙至少命中两个球”为事件B,由题意得:
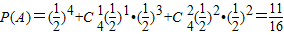
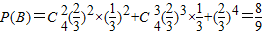
∴甲至多命中2个球且乙至少命中2个球的概率为:
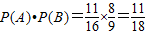
(Ⅱ)乙所得分数为η
η可能的取值-4,0,4,8,12,
P(η=-4)=
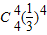 =
=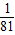 ,
,P(η=0)=
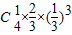 =
=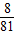
P(η=4)=C42
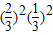 =
=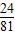
P(η=8)=
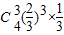 =
=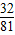
P(η=-4)=
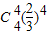 =
=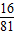
分布列如下:

∴Eη=
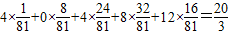 .
.点评:本题考查独立重复试验,考查离散型随机变量的分布列和期望,是一个综合题,解题时注意进球的个数对应的是乙所得的分数,注意分数与进球个数的对应.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙两名篮球运动员的投篮命中率分别为
与
,设甲投4球恰好进3球的概率为m,乙投3球恰好进2球的概率为n,则m与n的大小关系为( )
| 3 |
| 4 |
| 2 |
| 3 |
| A、m>n | B、m<n |
| C、m=n | D、m≥n |