题目内容
如图，已知A、B、C是椭圆E：
上的三点，其中点A的坐标为
，BC过椭圆的中心0，且AC⊥BC，
．
(I)求点C的坐标及椭圆E的方程；
(Ⅱ)若椭圆E上存在两点P、Q，使∠PCQ的平分线总是垂直于x轴，试叛断向量
是否共线，并给出证明。
解：（I）∵|BC|=2|AC|，且BC经过O（0，0），
∴|OC|=|AC|.
又
，
及C点坐标代入椭圆方程得
（II）关于椭圆上两点P、Q，
∵∠PCQ的平分线总垂直于x轴，
∵PC与CQ所在直线关于直线
对称，
设直线PC的斜率为k，则直线CQ的斜率为－k，
∴直线PC的方程为
，
即
①
直线CQ的方程为
②
将①代入
得
③
）在椭圆上， 
是方程③的一个根，
，
，
同理可得
，
又A（2
，0），
，
练习册系列答案
相关题目
17、如图，已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆（x-1）2+y2=1的交点，则|AB|•|CD|=
如图，已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆（x-1）2+y2=1的交点，则|AB|•|CD|等于（ ）
如图，已知A、B、C、D四点共圆，延长AD和BC相交于点E，AB=AC．
如图，已知A、B、C是长轴为4的椭圆上的三点，点A是长轴的右顶点，BC过椭圆中心O，且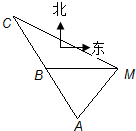
（2009•台州二模）如图，已知A、B、C是一条直路上的三点，一个人从A出发行走到B处时，望见塔M（将塔M视为与A、B、C在同一水平面上一点）在正东方向且A在东偏南α方向，继续行走1km在到达C处时，望见塔M在东偏南β方向，则塔M到直路ABC的最短距离为（ ）