题目内容
电信局为了配合客户不同需要,设有A、B两种方案.这两种方案应付话费(元)与通话时间(分钟)之间的关系如图所示(MN∥CD).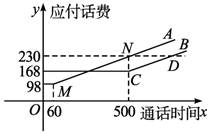
(1)若通话时间为2小时,按方案A、B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内方案B才会比方案A优惠?
分析:通过看图可得M、C、N三点坐标,从而求出两种方案的应付话费与通话时间的函数关系式.
解:由图知,M(60,98)、C(500,168)、N(500,230).
∵MN∥CD,
设这两方案的应付话费与通话时间的函数关系式分别为fA(x)、fB(x),
则fA(x)=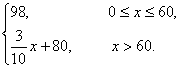
fB(x)=
(1)通话两小时的费用分别是116元和168元.
(2)fB(x+1)-fB(x)=0.3(x>500),或由直线CD的斜率的实际意义知方案B从500分钟以后每分钟收费0.3元.
(3)由图知:当0≤x≤60时,fA(x)<fB(x);当x>500时,fA(x)>fB(x);当60<x≤500时,由fA(x)>fB(x)得500≥x>![]() .综上可得通话时间在(
.综上可得通话时间在(![]() ,+∞)时方案B较优惠.
,+∞)时方案B较优惠.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
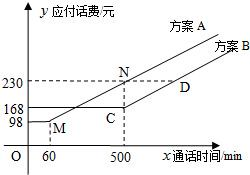 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.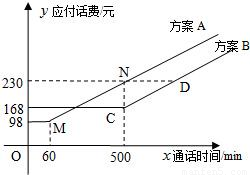 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.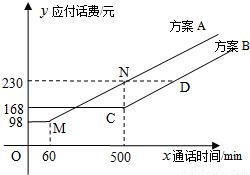 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.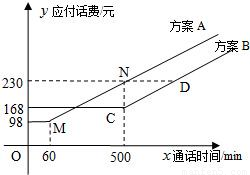 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.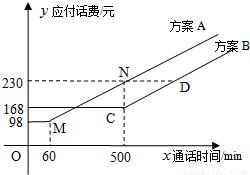 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD.