题目内容
已知向量 =(2sinx,2cosx),
=(2sinx,2cosx), =(
=( cosx,cosx),f(x)=
cosx,cosx),f(x)=
 ﹣1.
﹣1.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标先缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间[0,
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间[0, ]上的最小值.
]上的最小值.
 =(2sinx,2cosx),
=(2sinx,2cosx), =(
=( cosx,cosx),f(x)=
cosx,cosx),f(x)=
 ﹣1.
﹣1.(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间[0,
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间[0, ]上的最小值.
]上的最小值.解:(1)因为f(x)=2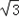 sinxcosx+2cos2x﹣1=
sinxcosx+2cos2x﹣1=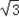 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+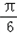 )
)
∴函数f(x)的最小正周期为T=π
由2kπ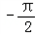
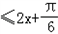
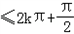 得
得
f(x)的单调递增区间为[k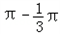 ,kπ
,kπ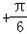 ],k∈Z
],k∈Z
(2)根据条件得g(x)=2sin(4x+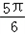 )
)
当x∈[0,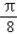 ]时,4x
]时,4x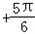 ∈[
∈[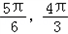 ],
],
所以当x= 时,
时,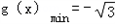
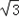 sinxcosx+2cos2x﹣1=
sinxcosx+2cos2x﹣1=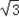 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+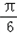 )
)∴函数f(x)的最小正周期为T=π
由2kπ
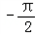
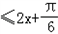
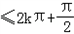 得
得f(x)的单调递增区间为[k
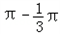 ,kπ
,kπ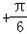 ],k∈Z
],k∈Z(2)根据条件得g(x)=2sin(4x+
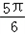 )
)当x∈[0,
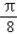 ]时,4x
]时,4x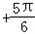 ∈[
∈[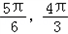 ],
],所以当x=
 时,
时,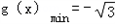

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 =(2sinωx,cos2ωx),向量
=(2sinωx,cos2ωx),向量 =(cosωx,
=(cosωx, ),其中ω>0,函数f(x)=
),其中ω>0,函数f(x)= •
• ,若f(x)图象的相邻两对称轴间的距离为π.
,若f(x)图象的相邻两对称轴间的距离为π. ,恒有|f(x)-m|<2成立,求实数m的取值范围.
,恒有|f(x)-m|<2成立,求实数m的取值范围. =(2cosα,2sinα),
=(2cosα,2sinα),  =(3cosβ,3sinβ),若
=(3cosβ,3sinβ),若 与圆
与圆 的位置关系是( )
的位置关系是( )