题目内容
17．已知△ABC中，a=1，b=c=4，求∠B和角平分线BD的长（D为AC与BD的交点）．分析 如图所示，取BC的中点E，连接AE，由b=c，可得AE⊥BC，∠B=∠C．利用cosB=$\frac{BE}{AB}$即可得出．由BD是∠B的角平分线，可得$\frac{CD}{AD}=\frac{BC}{AB}$，即可解出CD，在△BCE中，由余弦定理可得：BD2=BC2+CD2-2BC•CD•cosC，即可解出．
解答 解：如图所示，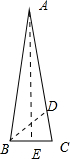
取BC的中点E，连接AE，∵b=c，
∴AE⊥BC，∠B=∠C．
∴cosB=$\frac{BE}{AB}$=$\frac{\frac{1}{2}}{4}$=$\frac{1}{8}$．
∵BD是∠B的角平分线，
则$\frac{CD}{AD}=\frac{BC}{AB}$，∴$\frac{CD}{AC}=\frac{BC}{AB+BC}$，
∴$\frac{CD}{4}=\frac{1}{5}$，解得CD=$\frac{4}{5}$．
在△BCE中，由余弦定理可得：BD2=BC2+CD2-2BC•CD•cosC=$1+（\frac{4}{5}）^{2}-2×1×\frac{4}{5}×\frac{1}{8}$=$\frac{36}{25}$，
∴BD=$\frac{6}{5}$．
点评 本题考查了等腰三角形的性质、角平分线的性质、直角三角形的边角关系、余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
7．设F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，P是C的右支上的点，射线PT平分∠F1PF2，过原点O作PT的平行线交PF1于点M，若|MP|=$\frac{1}{3}$|F1F2|，则C的离心率为（ ）
| A． | $\frac{3}{2}$ | B． | 3 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
如图，垂直于x轴的直线交双曲线 $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$于M，N两点，A1，A2为双曲线的左右顶点，求直线A1M与A2N的交点P的轨迹方程，并指出轨迹的形状．
如图，已知点S（-2，0）和圆O：x2+y2=4，ST是圆O的直经，从左到右M和N依次是ST的四等分点，P（异于S、T）是圆O上的动点，PD⊥ST，交ST于D，$\overrightarrow{PE}=λ\overrightarrow{ED}$，直线PS与TE交于C，|CM|+|CN|为定值．