题目内容
已知定义在R上的函数f(x)的图象关于点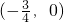 对称,且满足
对称,且满足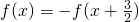 ,又f(-1)=1,f(0)=-2,则f(1)+f(2)+f(3)+…+f(2008)=________.
,又f(-1)=1,f(0)=-2,则f(1)+f(2)+f(3)+…+f(2008)=________.
解:因为函数f(x)满足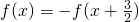 ,则f(x)=f(x+3)
,则f(x)=f(x+3)
又f(-1)=1,f(0)=-2,则f(-1)=f(-1+3)=f(2),又f(0)=f(0+3)=f(3).
又函数f(x)的图象关于点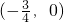 对称,
对称,
f(-1)=f(- )=f(-
)=f(- +
+ )=f(1)所以f(1)+f(2)+f(3)=0.
)=f(1)所以f(1)+f(2)+f(3)=0.
又f(1+3)=f(4),f(2+3)=f(5),f(3+3)=f(6)…又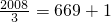 .
.
所以f(1)+f(2)+f(3)+…+f(2008)=f(1)=f(-1)=1
故答案为1.
分析:首先由函数且满足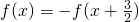 ,又f(-1)=1,f(0)=-2,可以分析得f(x)=f(x+3)即可求出f(2)和f(3).又函数f(x)的图象关于点
,又f(-1)=1,f(0)=-2,可以分析得f(x)=f(x+3)即可求出f(2)和f(3).又函数f(x)的图象关于点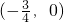 对称,又可推出f(-1)=f(1),综合考虑几个周期关系条件即可得到f(1)+f(2)+f(3)+…+f(2008)的值.
对称,又可推出f(-1)=f(1),综合考虑几个周期关系条件即可得到f(1)+f(2)+f(3)+…+f(2008)的值.
点评:此题主要考查函数的周期性问题,其中应用到函数关于点对称的性质,对于函数周期性这个考点考查的时候多和奇偶性,对称性问题综合考虑,技巧性较强.
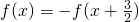 ,则f(x)=f(x+3)
,则f(x)=f(x+3)又f(-1)=1,f(0)=-2,则f(-1)=f(-1+3)=f(2),又f(0)=f(0+3)=f(3).
又函数f(x)的图象关于点
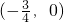 对称,
对称,f(-1)=f(-
 )=f(-
)=f(- +
+ )=f(1)所以f(1)+f(2)+f(3)=0.
)=f(1)所以f(1)+f(2)+f(3)=0.又f(1+3)=f(4),f(2+3)=f(5),f(3+3)=f(6)…又
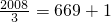 .
.所以f(1)+f(2)+f(3)+…+f(2008)=f(1)=f(-1)=1
故答案为1.
分析:首先由函数且满足
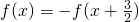 ,又f(-1)=1,f(0)=-2,可以分析得f(x)=f(x+3)即可求出f(2)和f(3).又函数f(x)的图象关于点
,又f(-1)=1,f(0)=-2,可以分析得f(x)=f(x+3)即可求出f(2)和f(3).又函数f(x)的图象关于点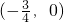 对称,又可推出f(-1)=f(1),综合考虑几个周期关系条件即可得到f(1)+f(2)+f(3)+…+f(2008)的值.
对称,又可推出f(-1)=f(1),综合考虑几个周期关系条件即可得到f(1)+f(2)+f(3)+…+f(2008)的值.点评:此题主要考查函数的周期性问题,其中应用到函数关于点对称的性质,对于函数周期性这个考点考查的时候多和奇偶性,对称性问题综合考虑,技巧性较强.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |