题目内容
设函数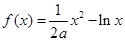 ,其中
,其中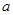 为大于零的常数.
为大于零的常数.
(1)当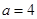 时,求函数
时,求函数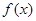 的单调区间和极值;
的单调区间和极值;
(2)若在区间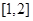 上至少存在一点
上至少存在一点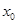 ,使得
,使得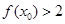 成立,求
成立,求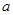 的取值范围.
的取值范围.
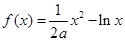 ,其中
,其中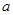 为大于零的常数.
为大于零的常数.(1)当
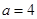 时,求函数
时,求函数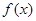 的单调区间和极值;
的单调区间和极值;(2)若在区间
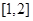 上至少存在一点
上至少存在一点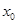 ,使得
,使得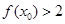 成立,求
成立,求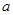 的取值范围.
的取值范围.(1)单调减区间为 ,极小值
,极小值 ,无极大值;(2)
,无极大值;(2) 
 .
.
 ,极小值
,极小值 ,无极大值;(2)
,无极大值;(2) 
 .
.(1)先求出导函数,然后再利用求极值的步骤逐步求解;(2)把问题转化为函数恒成立问题求解。
解:(1)当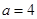 时,
时, (
( )
)
∴ (2分)
(2分)
令 ,得
,得 ,∴
,∴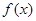 的单调增区间为
的单调增区间为 ,
,
令 ,得
,得 ,∴
,∴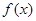 的单调减区间为
的单调减区间为 ,(4分)
,(4分)
∴当 时,
时,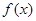 取极小值
取极小值 ,无极大值 (6分)
,无极大值 (6分)
(2)法一:原问题等价于在区间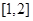 上至少存在一点
上至少存在一点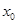 ,使得
,使得 成立,
成立,
令 ,即求
,即求 (8分)
(8分)
∵ 又
又 ,∴
,∴ 即
即 在区间
在区间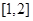 上单调递增,(12分)
上单调递增,(12分)
∴ ∴
∴
 (14分)
(14分)
法二:分类讨论方法按类给分
解:(1)当
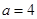 时,
时, (
( )
)∴
 (2分)
(2分)令
 ,得
,得 ,∴
,∴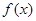 的单调增区间为
的单调增区间为 ,
,令
 ,得
,得 ,∴
,∴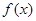 的单调减区间为
的单调减区间为 ,(4分)
,(4分)∴当
 时,
时,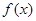 取极小值
取极小值 ,无极大值 (6分)
,无极大值 (6分)(2)法一:原问题等价于在区间
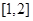 上至少存在一点
上至少存在一点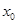 ,使得
,使得 成立,
成立,令
 ,即求
,即求 (8分)
(8分)∵
 又
又 ,∴
,∴ 即
即 在区间
在区间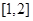 上单调递增,(12分)
上单调递增,(12分)∴
 ∴
∴
 (14分)
(14分)法二:分类讨论方法按类给分

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 ,求导函数
,求导函数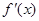 ,并确定
,并确定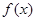 的单调区间.
的单调区间.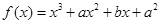 在
在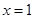 时有极值10,则实数
时有极值10,则实数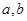 的值是( )
的值是( )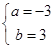

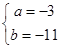 或
或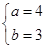
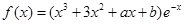
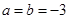 ,求
,求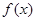 的单调区间;
的单调区间;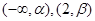 单调增加,在
单调增加,在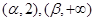 单调减少,
单调减少,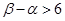
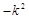 +1在区间(0,4)上是减函数,则的取值范围 ( )
+1在区间(0,4)上是减函数,则的取值范围 ( ) 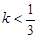
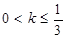
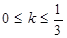
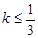
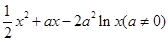 告xx+。一2a2 xre(a,“)·
告xx+。一2a2 xre(a,“)·