题目内容
2．已知tanθ=3，则$\frac{3sinθ+cosθ}{cosθ-3sinθ}$=（ ）| A． | $\frac{4}{5}$ | B． | $\frac{5}{4}$ | C． | -$\frac{4}{5}$ | D． | -$\frac{5}{4}$ |
分析 由条件利用同角三角函数的基本关系，求得所给式子的值．
解答 解：∵tanθ=3，则$\frac{3sinθ+cosθ}{cosθ-3sinθ}$=$\frac{3tanθ+1}{1-3tanθ}$=$\frac{9+1}{1-9}$=-$\frac{5}{4}$，
故选：D．
点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
相关题目
13．如图，若执行该程序，输出结果为48，则输入k值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
10．已知点P是边长为4的正方形内任一点，则点P到四个顶点的距离均大于2的概率是（ ）
| A． | $\frac{π}{4}$ | B． | 1-$\frac{π}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{π}{3}$ |
17．设集合M=$\{y|\frac{x^2}{25}+\frac{y^2}{9}=1\}$，N={x|2x+1≤1}，则M∩（∁RN）=（ ）
| A． | （3，+∞） | B． | （-2，-1] | C． | （-1，3] | D． | [-1，3） |
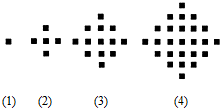某少数民族的刺绣有着悠久的历史，如图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（8，3）=2．如图是一个算法的程序框图，当输入的值为36时，则输出的结果为（ ）