题目内容
给出下列四个命题
(1).函数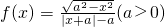 ,既不是奇函数,又不是偶函数;
,既不是奇函数,又不是偶函数;
(2)0<x<1,a,b∈R,且a•b>0,则函数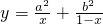 的最小值是a2+b2;
的最小值是a2+b2;
(3)已知向量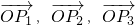 满足条件
满足条件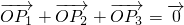 ,且
,且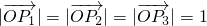 ,则△P1P2P3为正三角形;
,则△P1P2P3为正三角形;
(4)已知a>b>c,若不等式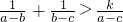 恒成立,则k∈(0,2);
恒成立,则k∈(0,2);
其中正确命题的有________(填出满足条件的所有序号)
解:(1)求函数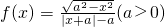 的定义域,为[-a,a],∴f(x)可化简为f(x)=
的定义域,为[-a,a],∴f(x)可化简为f(x)=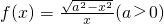
∴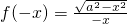 =-f(x),∴函数
=-f(x),∴函数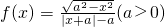 为奇函数,(1)错误.
为奇函数,(1)错误.
(2)∵0<x<1,∴0<1-x<1,∴函数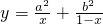 的函数值不可能等于a2+b2,∴(2)错误.
的函数值不可能等于a2+b2,∴(2)错误.
(3)∵向量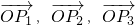 满足条件
满足条件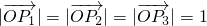 ,
,
∴点P1,P2,P3都在以O为圆心,半径是1的圆上,又∵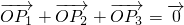 ,
,
∴三个向量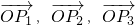 ,任两个所成角都为120°,
,任两个所成角都为120°,
∴△P1P2P3为正三角形,(3)正确.
(4)不等式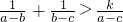 可变形为k<
可变形为k<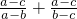 ,
,
∴若不等式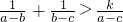 恒成立,则k一定小于
恒成立,则k一定小于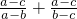 的最小值,
的最小值,
而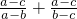 =
=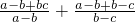 =
=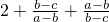 ≥4,∴k∈(-∞,40,∴(4)错误
≥4,∴k∈(-∞,40,∴(4)错误
故答案为(3)
分析:(1)利用函数奇偶性的定义,判断函数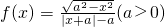 的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.
的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.
(2)因为0<x<1,所以0<1-x<1,所以函数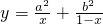 的函数值一定大于a2+b2,所以函数
的函数值一定大于a2+b2,所以函数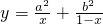 的最小值不是a2+b2.
的最小值不是a2+b2.
(3)通过条件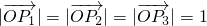 判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据
判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据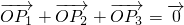 ,判断三个向量
,判断三个向量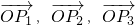 ,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.
,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.
(4)先把不等式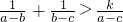 变形为k<
变形为k<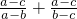 ,借助均值定理求出k的范围,与所给范围比较即可.
,借助均值定理求出k的范围,与所给范围比较即可.
点评:本题主要考查函数奇偶性的判断,应用均值定理求函数的最值,以及向量的加法运算的应用,属于综合题.
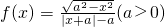 的定义域,为[-a,a],∴f(x)可化简为f(x)=
的定义域,为[-a,a],∴f(x)可化简为f(x)=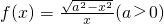
∴
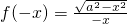 =-f(x),∴函数
=-f(x),∴函数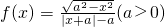 为奇函数,(1)错误.
为奇函数,(1)错误.(2)∵0<x<1,∴0<1-x<1,∴函数
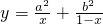 的函数值不可能等于a2+b2,∴(2)错误.
的函数值不可能等于a2+b2,∴(2)错误.(3)∵向量
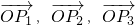 满足条件
满足条件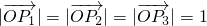 ,
,∴点P1,P2,P3都在以O为圆心,半径是1的圆上,又∵
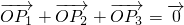 ,
,∴三个向量
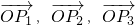 ,任两个所成角都为120°,
,任两个所成角都为120°,∴△P1P2P3为正三角形,(3)正确.
(4)不等式
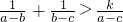 可变形为k<
可变形为k<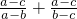 ,
,∴若不等式
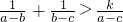 恒成立,则k一定小于
恒成立,则k一定小于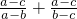 的最小值,
的最小值,而
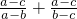 =
=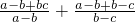 =
=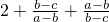 ≥4,∴k∈(-∞,40,∴(4)错误
≥4,∴k∈(-∞,40,∴(4)错误故答案为(3)
分析:(1)利用函数奇偶性的定义,判断函数
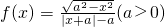 的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.
的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.(2)因为0<x<1,所以0<1-x<1,所以函数
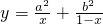 的函数值一定大于a2+b2,所以函数
的函数值一定大于a2+b2,所以函数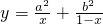 的最小值不是a2+b2.
的最小值不是a2+b2.(3)通过条件
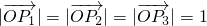 判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据
判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据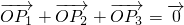 ,判断三个向量
,判断三个向量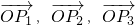 ,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.
,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.(4)先把不等式
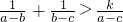 变形为k<
变形为k<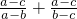 ,借助均值定理求出k的范围,与所给范围比较即可.
,借助均值定理求出k的范围,与所给范围比较即可.点评:本题主要考查函数奇偶性的判断,应用均值定理求函数的最值,以及向量的加法运算的应用,属于综合题.

练习册系列答案
相关题目