题目内容
过椭圆
+
=1内的点P（1，2）作两条互相垂直的弦AB，CD，若弦AB，CD的中点分别为M，N，则直线MN恒过定点，定点的坐标为
| x2 |
| 16 |
| y2 |
| 9 |
（
，
）
| 16 |
| 25 |
| 18 |
| 25 |
（
，
）
．| 16 |
| 25 |
| 18 |
| 25 |
分析：设A（x1，y1）、B（x2，y2），直线AB的方程为y-2=k（x-1），将其与椭圆消去y化简得（9+16k2）x2-32k（k-2）x+16（k-2）2-144=0，运用根与系数的关系算出M（
，
），同样理得出N（
，
），从而得到直线MN关于k为参数的两点式方程．分别取k=1和k=-1，得到动直线MN的两个位置，记为l1、l2，因为直线MN恒过定点，所以l1与l2的交点即为MN恒过的定点，由此联解直线l1与l2的方程组即可得到经过的定点坐标．
| 16k(k-2) |
| 9+16k2 |
| -9k+18 |
| 9+16k2 |
| 16+32k |
| 9k2+16 |
| 9k+18k2 |
| 9k2+16 |
解答：解：设直线AB的方程为y-2=k（x-1），与椭圆消去y得
（9+16k2）x2-32k（k-2）x+16（k-2）2-144=0
设A（x1，y1），B（x2，y2），AB中点为M（xM，yM）
∴x1+x2=
，可得xM=
（x1+x2）=
代入直线AB方程，得yM=
∴AB中点为M（
，
）
∵直线AB、CD互相垂直，∴用-
代替k，得CD中点为N（
，
）
因此，直线MN方程为
=
取k=1，得直线方程y-
=
(x+
)，记为l1； 再k=-1，得直线方程y-
=
(x-
)，记为l2．
∵随着直线AB、CD运动，直线MN恒过定点
∴直线l1与l2的交点即为MN恒过的定点，联解
，得
因此，直线MN恒过定点（
，
）
故答案为：（
，
）
（9+16k2）x2-32k（k-2）x+16（k-2）2-144=0
设A（x1，y1），B（x2，y2），AB中点为M（xM，yM）
∴x1+x2=
| 32k(k-2) |
| 9+16k2 |
| 1 |
| 2 |
| 16k(k-2) |
| 9+16k2 |
代入直线AB方程，得yM=
| -9k+18 |
| 9+16k2 |
∴AB中点为M（
| 16k(k-2) |
| 9+16k2 |
| -9k+18 |
| 9+16k2 |
∵直线AB、CD互相垂直，∴用-
| 1 |
| k |
| 16+32k |
| 9k2+16 |
| 9k+18k2 |
| 9k2+16 |
因此，直线MN方程为
y-
| ||||
|
x-
| ||||
|
取k=1，得直线方程y-
| 9 |
| 25 |
| 9 |
| 32 |
| 16 |
| 25 |
| 27 |
| 25 |
| 9 |
| 32 |
| 48 |
| 25 |
∵随着直线AB、CD运动，直线MN恒过定点
∴直线l1与l2的交点即为MN恒过的定点，联解
|
|
因此，直线MN恒过定点（
| 16 |
| 25 |
| 18 |
| 25 |
故答案为：（
| 16 |
| 25 |
| 18 |
| 25 |
点评：本题给出椭圆经过定点（1，2）的两条垂直的弦AB、CD，求由AB、CD中点确定的直线MN经过的定点坐标．着重考查了椭圆的标准方程与简单几何性质、直线与圆锥曲线的位置关系等知识，属于中档题．
练习册系列答案
相关题目
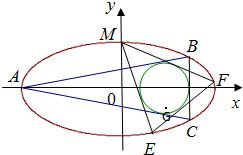如图，已知圆G：（x-2）2+y2=r2是椭圆