题目内容
已知O为坐标原点,点E,F的坐标分别为(-1,0)和(1,0),动点P满足: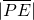 +
+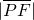 =4
=4
(1)求动点P的轨迹C的方程;
(2)过E点做直线与C相交于M,N两点,且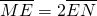 ,求直线MN的方程.
,求直线MN的方程.
解:(1)∵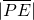 +
+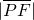 =4
=4
由椭圆的第一定义可知点P的轨迹为椭圆,
且2a=4,c=1,∴a2=4,b2=3
∴所求的椭圆方程为
(2)①当直线MN的斜率不存在时,不满足题意;
②当直线MN的斜率存在时,设其方程为y=k(x+1),
代入 化简得(3+4k2)x2+8k2x+4k2-12=0
化简得(3+4k2)x2+8k2x+4k2-12=0
设两交点的坐标为M(x1,y1)、N(x2,y2)
则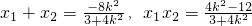
∵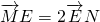 ,∴x1+2x2=-3
,∴x1+2x2=-3
∴ ,
,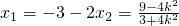
∴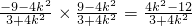
∴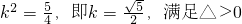
∴所求的直线MN的方程为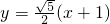
分析:(1)由椭圆的定义可知,到两个定点距离之和等于定长的点的轨迹为椭圆,所以所求点P的轨迹C为椭圆,再分别求出椭圆中a,b的值即可.
(2)当斜率存在时,设出直线MN的点斜式方程,与(1)中所求椭圆方程联立,求出x1+x2,x1x2,再根据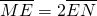 ,
,
即可求出k,得到直线MN的方程.
点评:本题主要考查了定义法求轨迹方程,以及直线与椭圆位置关系的判断.
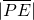 +
+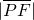 =4
=4由椭圆的第一定义可知点P的轨迹为椭圆,
且2a=4,c=1,∴a2=4,b2=3
∴所求的椭圆方程为

(2)①当直线MN的斜率不存在时,不满足题意;
②当直线MN的斜率存在时,设其方程为y=k(x+1),
代入
 化简得(3+4k2)x2+8k2x+4k2-12=0
化简得(3+4k2)x2+8k2x+4k2-12=0设两交点的坐标为M(x1,y1)、N(x2,y2)
则
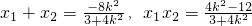
∵
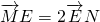 ,∴x1+2x2=-3
,∴x1+2x2=-3∴
 ,
,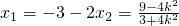
∴
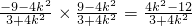
∴
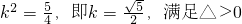
∴所求的直线MN的方程为
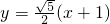
分析:(1)由椭圆的定义可知,到两个定点距离之和等于定长的点的轨迹为椭圆,所以所求点P的轨迹C为椭圆,再分别求出椭圆中a,b的值即可.
(2)当斜率存在时,设出直线MN的点斜式方程,与(1)中所求椭圆方程联立,求出x1+x2,x1x2,再根据
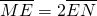 ,
,即可求出k,得到直线MN的方程.
点评:本题主要考查了定义法求轨迹方程,以及直线与椭圆位置关系的判断.

练习册系列答案
相关题目