题目内容
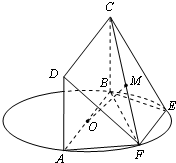 如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.(1)求证:AF⊥平面CBF.
(2)设FC的中点为M,求证:OM∥平面DAF.
(3)求四棱锥F-ABCD的体积.
分析:(Ⅰ)欲证AF⊥平面CBF,根据直线与平面垂直的判定定理可知只需证AF与平面CBF内两相交直线垂直,根据面面垂直的性质可知CB⊥平面ABEF,而AF?平面ABEF,则AF⊥CB,而AF⊥BF,满足定理所需条件;
(Ⅱ)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可,设DF的中点为N,则MNAO为平行四边形,则OM∥AN,又AN?平面DAF,OM不属于平面DAF,满足定理所需条件;
(Ⅲ)过点F作FG⊥AB于G,根据面面垂直的性质可知FG⊥平面ABCD,FG即正△OEF的高,然后根据三棱锥的体积公式进行求解即可.
(Ⅱ)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可,设DF的中点为N,则MNAO为平行四边形,则OM∥AN,又AN?平面DAF,OM不属于平面DAF,满足定理所需条件;
(Ⅲ)过点F作FG⊥AB于G,根据面面垂直的性质可知FG⊥平面ABCD,FG即正△OEF的高,然后根据三棱锥的体积公式进行求解即可.
解答:解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB
∴CB⊥平面ABEF∵AF?平面ABEF
∴AF⊥CB
又AB为圆O的直径∴AF⊥BF
∴AF⊥平面CBF
(Ⅱ)设DF的中点为N,则MN
CD又AO
CD,
∴MN
AO∴MNAO为平行四边形
∴OM∥AN,
又AN?平面DAF,OM不属于平面DAF
∴OM∥平面DAF
(Ⅲ)过点F作FG⊥AB于G∵平面ABCD⊥平面ABEF,
∴FG⊥平面ABCD,FG即正△OEF的高
∴FG=
∴SABCD=2
∴VF-ABCD=
SABCD•FG=
FG=
平面ABCD∩平面ABEF=AB
∴CB⊥平面ABEF∵AF?平面ABEF
∴AF⊥CB
又AB为圆O的直径∴AF⊥BF
∴AF⊥平面CBF
(Ⅱ)设DF的中点为N,则MN
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |

∴MN
| ||
. |
∴OM∥AN,
又AN?平面DAF,OM不属于平面DAF
∴OM∥平面DAF
(Ⅲ)过点F作FG⊥AB于G∵平面ABCD⊥平面ABEF,
∴FG⊥平面ABCD,FG即正△OEF的高
∴FG=
| ||
| 2 |
∴VF-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题主要考查直线与平面平行的判定,以及直线与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
相关题目


 .
. ;
; ;
; ,求
,求 的值.
的值.




 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数